题目内容
10.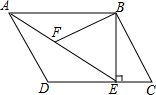 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.下列结论:
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.下列结论:①△ABE与△CBE相似;②$\frac{DC}{AE}=\frac{BF}{BC}$;③∠ABF=∠DAE;④DE=BC;
其中正确的是( )
| A. | ①②③④ | B. | ②③ | C. | ②④ | D. | ③ |
分析 ①在平行四边形ABCD中,根据平行线的性质得到BE⊥CD,于是得到∠ABE=∠BEC=90°,由于只有一对角对应相等,于是得到△ABE与△CBE不一定相似;故①错误;②根据平行线的性质得到∠BAF=∠AED,∠D+∠C=180°,由已知条件得到∠AFB+∠BFE=180°∠BFE=∠C,求得∠AFB=∠D,推出△ABF∽△ADE,于是得到$\frac{AB}{AE}=\frac{BF}{AD}$,等量代换得到$\frac{DC}{AE}=\frac{BF}{BC}$,故②正确;③根据相似三角形的性质即可得到∠ABF=∠DAE;故③正确;④由于AD=BC,DE不一定等于AD,于是得到DE不一定等于BC,故④错误.
解答 证明:①在平行四边形ABCD中,
∵AB∥CD,
∵BE⊥CD,
∴BE⊥AB,
∴∠ABE=∠BEC=90°,
∴只有一对角对应相等,
∴△ABE与△CBE不一定相似;故①错误;
②∵AB∥CD,AD∥BC,
∴∠BAF=∠AED,∠D+∠C=180°,
∵∠AFB+∠BFE=180°∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△ADE,
∴$\frac{AB}{AE}=\frac{BF}{AD}$,
∵CD=AB,BC=AD,
∴$\frac{DC}{AE}=\frac{BF}{BC}$,故②正确;
③∵△ABF∽△ADE,
∴∠ABF=∠DAE;故③正确;
④∵AD=BC,DE不一定等于AD,
∴DE不一定等于BC,故④错误.
故选B.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{8}÷\sqrt{2}$=4 | C. | $\sqrt{27}$=3$\sqrt{3}$ | D. | (1+$\sqrt{2})(1-\sqrt{2})=1$(1-$\sqrt{2}$)=1 |
18. 抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.
抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.
 抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.
抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.关于x的分式方程$\frac{m}{x-5}$=1,下列说法正确的是( )
| A. | m<-5时,方程的解为负数 | B. | m>-5时,方程的解是正数 | ||
| C. | 方程的解是x=m+5 | D. | 无法确定 |
15.在下表的空白处填上适当的数,使各横行与各竖列的4个数之和相等.
| 1 | -3 | -4 | 6 |
| -2 | +7 | ||
| 5 | -8 | ||
| -10 | 9 |
20.某商人在一次买卖中均以168元卖出两套服装,其中一套盈利20%,另一套亏本20%,该商贩在这次经营中( )
| A. | 亏本14元 | B. | 盈利14元 | C. | 不亏不盈 | D. | 盈利20元 |
 如图,已知OA=OB.
如图,已知OA=OB. 如图,等边三角形ABC的边长为4,高为h.
如图,等边三角形ABC的边长为4,高为h.