题目内容
7.若等腰三角形的一个内角是40°,则它的顶角是( )| A. | 100° | B. | 40° | C. | 100°或40° | D. | 60° |
分析 已知等腰三角形的一个内角为40°,根据等腰三角形的性质可分情况解答:当40°是顶角或者40°是底角两种情况.
解答 解:此题要分情况考虑:
①40°是它的顶角;
②40°是它的底角,则顶角是180°-40°×2=100°.
所以这个等腰三角形的顶角为40°或100°.
故选C.
点评 本题考查了等腰三角形的性质及三角形内角和定理;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
18.已知x,y满足$\left\{\begin{array}{l}{2x-3y=1①}\\{3x-2y=5②}\end{array}\right.$,如果①×a+②×b可整体得到x+11y的值,那么a,b的值可以是( )
| A. | a=2,b=-1 | B. | a=-4,b=3 | C. | a=1,b=-7 | D. | a=-7,b=5 |
2.下列运算正确的是( )
| A. | a2•a2=a4 | B. | (a-b)2=a2-b2 | C. | 2+$\sqrt{2}$=2$\sqrt{2}$ | D. | (-a3)2=-a6 |
16.下列关于多边形的说法不正确的是( )
| A. | 内角和与外角和相等的多边形是四边形 | |
| B. | 十边形的内角和为1440° | |
| C. | 多边形的内角中最多有四个直角 | |
| D. | 十边形共有40条对角线 |
17.已知|x+y-3|+(x-2y)2=0,则( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
 如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.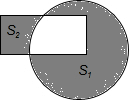 如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π)
如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π) 如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.
如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.