题目内容
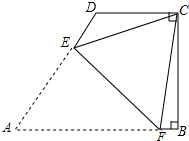 如图,在直角梯形ABCD中,∠ABC=∠BCD=90°,AD=AB,∠DAB=60°,点E、F分别在AD、AB边上,将梯形ABCD沿直线EF折叠,此时点A与点C重合,若DC=4,则线段BF的长为
如图,在直角梯形ABCD中,∠ABC=∠BCD=90°,AD=AB,∠DAB=60°,点E、F分别在AD、AB边上,将梯形ABCD沿直线EF折叠,此时点A与点C重合,若DC=4,则线段BF的长为考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线;证明△ABD为等边三角形,进而得到AB=BD,∠ABD=60°;求出BD=8,BC=4
,此为解题的关键性结论;列出关于BF的方程,即可解决问题.
| 3 |
解答: 解:如图,连接BD;
解:如图,连接BD;
∵AD=AB,∠DAB=60°,
∴△ABD为等边三角形,
∴AB=BD,∠ABD=60°;
∴∠DBC=90°-60°=30°;
∵∠BCD=90°,
∴BD=2DC=8,BC=4
;
由题意得:AF=CF(设为λ),
则BF=8-λ;
由勾股定理得:λ2=(8-λ)2+(4
)2,
解得:λ=7,
∴线段BF的长为1,
故答案为1.
 解:如图,连接BD;
解:如图,连接BD;∵AD=AB,∠DAB=60°,
∴△ABD为等边三角形,
∴AB=BD,∠ABD=60°;
∴∠DBC=90°-60°=30°;
∵∠BCD=90°,
∴BD=2DC=8,BC=4
| 3 |
由题意得:AF=CF(设为λ),
则BF=8-λ;
由勾股定理得:λ2=(8-λ)2+(4
| 3 |
解得:λ=7,
∴线段BF的长为1,
故答案为1.
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用翻折变换的性质、勾股定理等几何知识点来分析、解答.

练习册系列答案
相关题目
 如图所示,已知PA=PB,∠1+∠2=180°.求证:OP平分∠AOB.
如图所示,已知PA=PB,∠1+∠2=180°.求证:OP平分∠AOB.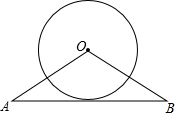 已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切.
已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切. 如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AE,AC=AE.
如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AE,AC=AE.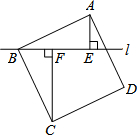 如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为
如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为