题目内容
17.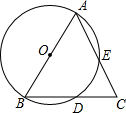 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D、E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D、E.(1)求证:BD=CD;
(2)若AB=8,∠A=60°,求弓形AE的面积.
分析 (1)连接AD,根据圆周角定理的推论得到∠BDA=90°,再根据等腰三角形的性质即可得到BD=CD;
(2)连接OE,先求得∠AOE,再用扇形AOE的面积减去△AOE的面积即可得出弓形AE的面积.
解答 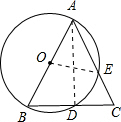 证明:(1)连接AD,
证明:(1)连接AD,
∵AB为⊙O的直径,
∴∠BDA=90°,
∴AD⊥BC.
∵AB=AC.
∴BD=CD;
(2)连接OE,
∵AB=8,∠A=60°,
∴OA=OE=4,∠AOE=60°,
∴S弓形AE=S扇形AOE-S△AOE=$\frac{60π×{4}^{2}}{360}$-$\frac{1}{2}$×4×2$\sqrt{3}$=$\frac{8}{3}$π-4$\sqrt{3}$.
点评 本题考查了扇形面积和等腰三角形的性质以及圆周角定理的推论:直径所对的圆周角为直角.掌握扇形的面积公式、三角形的面积公式以及弓形的面积公式是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
8.一个多边形的边数每增加一条,这个多边形的( )
| A. | 内角和增加 180° | B. | 外角和增加 360° | C. | 对角线增加一条 | D. | 内角和增加 360° |
2. 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )| A. | $\sqrt{2}$ | B. | 1.5 | C. | $\sqrt{3}$ | D. | 2 |
 如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为$\frac{24}{5}$cm.
如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为$\frac{24}{5}$cm. 如图,在△ABC中,∠BAC>90°,AB的垂直平分线MP交BC于点P,AC的垂直平分线NQ交BC于点Q,连接AP,AQ,若△APQ的周长为20cm,则BC为20cm.
如图,在△ABC中,∠BAC>90°,AB的垂直平分线MP交BC于点P,AC的垂直平分线NQ交BC于点Q,连接AP,AQ,若△APQ的周长为20cm,则BC为20cm. 已知:如图,在?BEDF中,点A、C在对角线EF所在的直线上,且AE=CF.求证:四边形ABCD是平行四边形.
已知:如图,在?BEDF中,点A、C在对角线EF所在的直线上,且AE=CF.求证:四边形ABCD是平行四边形.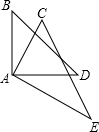 将一副三角板如图摆放,若∠BAC=31°45′,则∠EAD的度数是31°45′.
将一副三角板如图摆放,若∠BAC=31°45′,则∠EAD的度数是31°45′.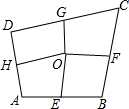 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG=5.
如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG=5.