��Ŀ����
11��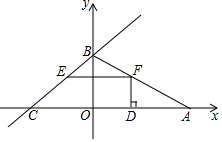 ��ͼ����ֱ֪��y=$\frac{3}{4}$x+3�������ύ��B��C���㣬��A��x����������һ�㣬����S��ABC=15����F���߶�AB��һ���㣨����˵��غϣ�������F��FE��x�ᣬ��BC��E��
��ͼ����ֱ֪��y=$\frac{3}{4}$x+3�������ύ��B��C���㣬��A��x����������һ�㣬����S��ABC=15����F���߶�AB��һ���㣨����˵��غϣ�������F��FE��x�ᣬ��BC��E����1����AB����ֱ�ߵĽ���ʽ��
��2����FD��x����D���ҵ�D������Ϊ��m��0�������ú�m�Ĵ���ʽ��ʾDF��EF�ij���
��3����x�����Ƿ����һ��P��ʹ�á�PEFΪ����ֱ�������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1����ֱ��y=$\frac{3}{4}$x+3�����B��C���꣬�ٽ��S��ABC=15��������A�����꣬���ô���ϵ���������ֱ��AB�Ľ���ʽ��
��2������ֱ��AB����ʽ�����F��������꣬���ɱ�ʾ��DF�ij�����EF��x����ɵó�E�������꣬����ֱ��BC����ʽ�����E������꣬�Ӷ��ɱ�ʾ��EF�ij���
��3����P��t��0��������PFE=90��ʱ������PF=EF����ɵõ�����x�ķ��̣������P�����ꣻ����PEF=90��ʱ������PE=EF=DF�������P�����ꣻ����EPF=90��ʱ����P��PH��EF���ɵ���ֱ�������ε����ʿ�֪PH=$\frac{1}{2}$EF�������D�����꣬�Ӷ������P�����꣮
��� �⣺
��1����y=$\frac{3}{4}$x+3�У���x=0�ɵ�y=3����y=0�����x=-4��
��B��0��3����C��-4��0����
��OB=3��OC=4��
��S��ABC=15��
��$\frac{1}{2}$AC•OB=15����$\frac{1}{2}$��OA+4����3=15�����OA=6��
��A��6��0����
��ֱ��AB����ʽΪy=kx+b��
��$\left\{\begin{array}{l}{6k+b=0}\\{b=3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$��
��ֱ��AB����ʽΪy=-$\frac{1}{2}$x+3��
��2����FD��x�ᣬ��D��m��0����
��F�������Ϊm��
��y=-$\frac{1}{2}$x+3�У���x=m���ɵ�y=-$\frac{1}{2}$m+3��
��DF=-$\frac{1}{2}$m+3��
��EF��x�ᣬ
��E��������Ϊ-$\frac{1}{2}$m+3��
��y=$\frac{3}{4}$x+3�У���y=-$\frac{1}{2}$m+3���ɵ�-$\frac{1}{2}$m+3=$\frac{3}{4}$x+3�����x=-$\frac{2}{3}$m��
��F���߶�AB�ϣ�
��0��m��6
��EF=m+$\frac{2}{3}$m=$\frac{5}{3}$m��
��3������������������ĵ�P����������Ϊ��t��0����
�ߡ�PEFΪ����ֱ�������Σ�
���С�PFE=90�㡢��PEF=90��͡�EPF=90�����������
�ٵ���PFE=90��ʱ������PF=EF��
�ɣ�2���ɵ�PF=-$\frac{1}{2}$t+3��EF=$\frac{5}{3}$t��
��-$\frac{1}{2}$t+3=$\frac{5}{3}$t�����t=$\frac{18}{13}$��
��P��$\frac{18}{13}$��0����
�ڵ���PEF=90��ʱ������PE=EF��
��y=$\frac{3}{4}$x+3�У���x=t�ɵ�y=$\frac{3}{4}$t+3��
��PE=$\frac{3}{4}$t+3��
��y=-$\frac{1}{2}$x+3�У���y=$\frac{3}{4}$t+3���ɵ�$\frac{3}{4}$t+3=-$\frac{1}{2}$x+3�����x=-$\frac{3}{2}$t��
��EF=-t+��-$\frac{3}{2}$t��=-$\frac{5}{2}$t��
��$\frac{3}{4}$t+3=-$\frac{5}{2}$t�����t=-$\frac{12}{7}$��
��P��-$\frac{12}{7}$��0����
�۵���EPF=90��ʱ����ͼ����P��PH��EF�ڵ�H����PH=HF=PD=EH=DF��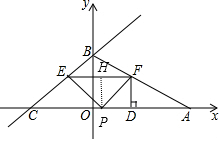
�ɣ�2����֪DF=-$\frac{1}{2}$m+3��EF=$\frac{5}{3}$m��
��-$\frac{1}{2}$m+3=$\frac{1}{2}$��$\frac{5}{3}$m�����m=$\frac{9}{4}$��
��PD=DF=-$\frac{1}{2}$��$\frac{9}{4}$+3=$\frac{15}{8}$��OD=$\frac{9}{4}$��
��OP=OD-PD=$\frac{9}{4}$-$\frac{15}{8}$=$\frac{3}{8}$��
��P��$\frac{3}{8}$��0����
���Ͽ�֪�������������ĵ�P��������Ϊ��$\frac{18}{13}$��0����-$\frac{12}{7}$��0����P��$\frac{3}{8}$��0����
���� ����Ϊһ�κ������ۺ�Ӧ�ã��漰�����ε����������ϵ����������ͼ���ϵ����������������ֱ�������ε����ʡ�����˼�뼰��������˼�룮�ڣ�1�������A�������ǽ���Ĺؼ����ڣ�2���зֱ��ʾ��E��F�������ǽ���Ĺؼ����ڣ�3����ȷ����P���λ�ã����õ���ֱ�������ε����ʵõ�����P������ķ����ǽ���Ĺؼ���ע���������������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�| ����x/�� | 0 | 5 | 10 | 15 | 20 |
| ����y/��m/s�� | 331 | 334 | 337 | 340 | 343 |
��2��xÿ����5�棬y�ı仯�����ͬ��
��3����������Ϊ25��ʱ�����Ƕ��٣�
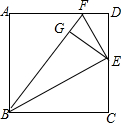 ��ͼ��������ABCD�У���E��CD���е㣬DF=$\frac{1}{4}$AD��EG��BF��G����֤��BE2=BG•BF��
��ͼ��������ABCD�У���E��CD���е㣬DF=$\frac{1}{4}$AD��EG��BF��G����֤��BE2=BG•BF��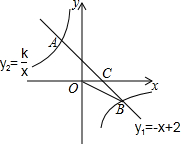 ��ͼ��һ�κ���y1=-x+2��ͼ���뷴��������y2=$\frac{k}{x}$��ͼ���ཻ��A��B���㣬��x���ཻ�ڵ�C����֪��B��������Ϊ-2��
��ͼ��һ�κ���y1=-x+2��ͼ���뷴��������y2=$\frac{k}{x}$��ͼ���ཻ��A��B���㣬��x���ཻ�ڵ�C����֪��B��������Ϊ-2��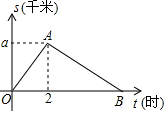 ij��λ��С�̹Ⱦٰ조�����Ž�һ���ס�ͽ�����ij�˴�����������4ǧ��/Сʱ��ƽ���ٶ�����2Сʱ�����յ㣬֮������ԭ·���أ�������뿪����·��s��ǧ�ף��벽��ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ������ͼ���ṩ��Ϣ������������⣺
ij��λ��С�̹Ⱦٰ조�����Ž�һ���ס�ͽ�����ij�˴�����������4ǧ��/Сʱ��ƽ���ٶ�����2Сʱ�����յ㣬֮������ԭ·���أ�������뿪����·��s��ǧ�ף��벽��ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ������ͼ���ṩ��Ϣ������������⣺ ��ͼ����E=��F=90�㣬��B=��C��AE=AF���������н��ۣ��١�1=��2����BE=CF���ۡ�ACN�ա�ABM����CD=DN��������ȷ���Ǣ٢ڢۣ�����ţ������д���Ľ������Ϊ��ȷ�ģ�CD=BD����û������ޡ���
��ͼ����E=��F=90�㣬��B=��C��AE=AF���������н��ۣ��١�1=��2����BE=CF���ۡ�ACN�ա�ABM����CD=DN��������ȷ���Ǣ٢ڢۣ�����ţ������д���Ľ������Ϊ��ȷ�ģ�CD=BD����û������ޡ��� ��ͼ����֪����y=2x��y=ax-3��ͼ���ڵ�P��-1��-2���������ͼ��ɵò���ʽ2x-ax+3��0�Ľ⼯��-1��
��ͼ����֪����y=2x��y=ax-3��ͼ���ڵ�P��-1��-2���������ͼ��ɵò���ʽ2x-ax+3��0�Ľ⼯��-1��