题目内容
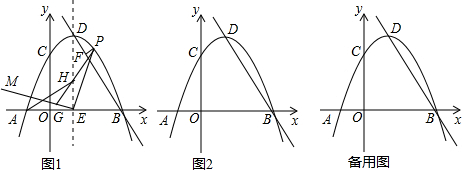
16. 如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的是①②③(填序号).若有错误的结论请改为正确的:CD=BD(若没有请填“无”)
如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的是①②③(填序号).若有错误的结论请改为正确的:CD=BD(若没有请填“无”)
分析 根据三角形的内角和定理求出∠EAB=∠FAC,即可判断①;根据AAS证△EAB≌△FAC,即可判断②;推出AC=AB,根据ASA即可证出③;不能推出CD和DN所在的三角形全等,也不能用其它方法证出CD=DN.
解答 解:∵∠E=∠F=90°,∠B=∠C,
∵∠E+∠B+∠EAB=180°,∠F+∠C+∠FAC=180°,
∴∠EAB=∠FAC,
∴∠EAB-CAB=∠FAC-∠CAB,
即∠1=∠2,∴①正确;
在△EAB和△FAC中
$\left\{\begin{array}{l}{∠B=∠C}\\{∠E=∠F}\\{AE=AF}\end{array}\right.$,
∴△EAB≌△FAC,
∴BE=CF,AC=AB,∴②正确;
在△ACN和△ABM中
$\left\{\begin{array}{l}{∠C=∠B}\\{AC=AB}\\{∠CAN=∠MBA}\end{array}\right.$,
∴△ACN≌△ABM,∴③正确;
∵根据已知不能推出CD=DN,∴④错误;
应该是CD=BD.
∴正确的结论有①②③,
故答案为①②③,CD=BD.
点评 本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力和辨析能力,题目比较好,难度适中.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
7.下列运用等式的性质进行变形,正确的是( )
| A. | 如果a=b,那么a+c=b-c | B. | 如果ac=bc,那么a=b | ||
| C. | 如果a=b,那么a(c2+1)=b(c2+1) | D. | 如果ab=3b,那么a=3 |
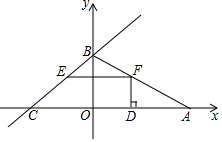 如图,已知直线y=$\frac{3}{4}$x+3与坐标轴交于B,C两点,点A是x轴正半轴上一点,并且S△ABC=15,点F是线段AB上一动点(不与端点重合),过点F作FE∥x轴,交BC于E.
如图,已知直线y=$\frac{3}{4}$x+3与坐标轴交于B,C两点,点A是x轴正半轴上一点,并且S△ABC=15,点F是线段AB上一动点(不与端点重合),过点F作FE∥x轴,交BC于E. 图中一共有6个角.
图中一共有6个角.