题目内容
2．先化简，再求值：（$\frac{2}{x-1}$+$\frac{1}{x+1}$）•（x2-1），其中x=$\frac{1}{3}$．分析 根据分式的加法和乘法可以化简题目中的式子，然后将x的值代入即可解答本题．
解答 解：（$\frac{2}{x-1}$+$\frac{1}{x+1}$）•（x2-1）
=$\frac{2（x+1）+（x-1）}{（x-1）（x+1）}•（x+1）（x-1）$
=2（x+1）+（x-1）
=2x+2+x-1
=3x+1，
当x=$\frac{1}{3}$时，原式=3×$\frac{1}{3}$+1=1+1=2．
点评 本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
练习册系列答案
相关题目
如图，菱形DABC的顶点D是原点，顶点B到y轴上，菱形的两条对角线分别是6和4，反比例函数y=$\frac{k}{x}$（x＜0）的图象经过点C，则k的值为-6．
7．下列运用等式的性质进行变形，正确的是（ ）
| A． | 如果a=b，那么a+c=b-c | B． | 如果ac=bc，那么a=b | ||
| C． | 如果a=b，那么a（c2+1）=b（c2+1） | D． | 如果ab=3b，那么a=3 |
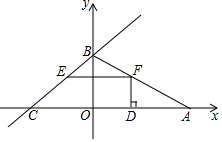如图，已知直线y=$\frac{3}{4}$x+3与坐标轴交于B，C两点，点A是x轴正半轴上一点，并且S△ABC=15，点F是线段AB上一动点（不与端点重合），过点F作FE∥x轴，交BC于E．