题目内容
19.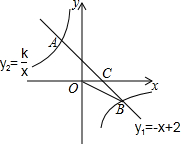 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C,已知点B的纵坐标为-2.
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C,已知点B的纵坐标为-2.(1)求反比例函数的解析式;
(2)已知S△AOB的面积为6,则A(-2,4);
(3)当y1<y2时,直接写出x的取值范围.
分析 (1)利用一次函数y1=-x+2的图象经过点B,可得B(4,-2),把B(4,-2)代入反比例函数y2=$\frac{k}{x}$,可得反比例函数的解析式;
(2)设点A(a,b),根据S△AOB的面积为6,可得$\frac{1}{2}$OC(|b|+|-2|)=6,进而得到b的值,再根据反比例函数解析式,即可得到点A的坐标;
(3)根据一次函数y1=-x+2的图象在反比例函数y2=$\frac{k}{x}$的图象下方,可得对应的自变量x的取值范围.
解答 解:(1)在一次函数y1=-x+2中,令y=-2,可得
-2=-x+2,
解得x=4,
∴B(4,-2),
把B(4,-2)代入反比例函数y2=$\frac{k}{x}$,可得
k=-2×4=-8,
∴反比例函数的解析式为y=-$\frac{8}{x}$;
(2)设点A(a,b),则
由S△AOB的面积为6,可得$\frac{1}{2}$OC(|b|+|-2|)=6,
∴$\frac{1}{2}$×2×(|b|+2)=6,
解得b=4,(负值已舍去)
又∵ab=-8,
∴a=-2,
∴A(-2,4),
故答案为:-2,4;
(3)∵A(-2,4),B(4,-2),
∴当y1<y2时,-2<x<0或x>4.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及数形结合思想的运用.

练习册系列答案
相关题目
7.下列运用等式的性质进行变形,正确的是( )
| A. | 如果a=b,那么a+c=b-c | B. | 如果ac=bc,那么a=b | ||
| C. | 如果a=b,那么a(c2+1)=b(c2+1) | D. | 如果ab=3b,那么a=3 |

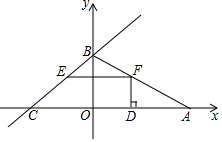 如图,已知直线y=$\frac{3}{4}$x+3与坐标轴交于B,C两点,点A是x轴正半轴上一点,并且S△ABC=15,点F是线段AB上一动点(不与端点重合),过点F作FE∥x轴,交BC于E.
如图,已知直线y=$\frac{3}{4}$x+3与坐标轴交于B,C两点,点A是x轴正半轴上一点,并且S△ABC=15,点F是线段AB上一动点(不与端点重合),过点F作FE∥x轴,交BC于E.