题目内容
已知：如图，点A、B、D、E在同一直线上，AD=EB，AC=EF，AC∥EF．求证：BC=DF．考点：全等三角形的判定与性质
专题：证明题
分析：根据AC∥EF证得∠A=∠E，然后根据AD=EB得到AB=ED，利用SAS证明两三角形全等即可．
解答：证明：∵AD=EB，
∴AD-BD=EB-BD．
即AB=ED．
∵AC∥EF，
∴∠A=∠E．
在△ABC和△EDF中，
∴△ABC≌△EDF（SAS），
∴BC=DF．
∴AD-BD=EB-BD．
即AB=ED．
∵AC∥EF，
∴∠A=∠E．
在△ABC和△EDF中，
|
∴△ABC≌△EDF（SAS），
∴BC=DF．
点评：本题考查了全等三角形的判定与性质，解题的关键是选择最合适的方法证明两三角形全等．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
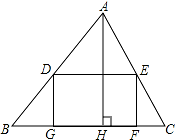如图，△ABC中，BC=80mm，AH=60mm，D在AB边上，E在AC上，DE∥BC以DE为边在△ABC内作矩形DEFG，设DE=x，DG=y．
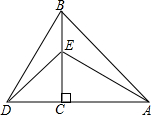如图，△ACB与△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在BC上，连接AE，BD．
如图，直线AB，CD相交于点O，EO⊥CD于点O，FO⊥AB于点O，∠DOF=65°，求∠BOE的度数．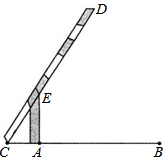
如图，小明在研究性学习活动中，对自己家所在的小区进行调查后发现，小区汽车入口宽AB为3.2m，在入口的一侧安装了停止杆CD，其中AE为支架．当停止杆仰起并与地面成60°角时，停止杆的端点C恰好与地面接触．此时CA为0.7m．在此状态下，若一辆货车高3m，宽2.5m，入口两侧不能通车，那么这辆货车在不碰杆的情况下，能从入口内通过吗？请你通过估算说明．（参考数据：
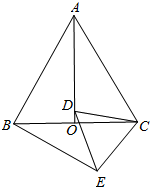如图，等边△ABC中，AO是∠BAC的角平分线，D为AO上一点，以CD为一边且在CD下方作等边△CDE，连接BE．
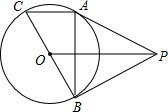如图，P为⊙O外一点，PA、PB均为⊙O的切线，A和B是切点，BC是直径．求证：