题目内容
 如图,AB=AC,BD=CD,延长DB至M,使MB=
如图,AB=AC,BD=CD,延长DB至M,使MB=| 1 |
| 2 |
| 1 |
| 2 |
考点:全等三角形的判定与性质
专题:证明题
分析:连接AD,根据全等三角形的判定(SSS)可证到△ABD≌△ACD,则有∠ABD=∠ACD,再根据等角的补角相等可得∠ABM=∠ACN.易证BM=CN,根据全等三角形的判定(SAS)即可证到△ABM≌△ACN,则有∠MAB=∠NAC.
解答:解:连接AD,如图.
在△ABD和△ACD中,
,
∴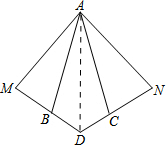 △ABD≌△ACD,
△ABD≌△ACD,
∴∠ABD=∠ACD.
∵∠ABD+∠ABM=180°,∠ACD+∠ACN=180°,
∴∠ABM=∠ACN.
∵MB=
AB,NC=
AC,AB=AC,
∴MB=NC.
在△ABM和△ACN中,
,
∴△ABM≌△ACN,
∴∠MAB=∠NAC.
在△ABD和△ACD中,
|
∴
 △ABD≌△ACD,
△ABD≌△ACD,∴∠ABD=∠ACD.
∵∠ABD+∠ABM=180°,∠ACD+∠ACN=180°,
∴∠ABM=∠ACN.
∵MB=
| 1 |
| 2 |
| 1 |
| 2 |
∴MB=NC.
在△ABM和△ACN中,
|
∴△ABM≌△ACN,
∴∠MAB=∠NAC.
点评:本题主要考查了全等三角形的判定与性质、等角的补角相等等知识,要证明两个角(或两条线段)相等,通常可以考虑证它们所在的两个三角形全等.

练习册系列答案
相关题目
在数-32、|-2.5|、-(-2
)、(-3)3中,负数的个数是( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
 如图,正方形ABCD的边长为4,点P,Q,R,S分别在AB,BC,CD,DA上,且BQ=2AP,CR=3AP,DS=4AP.
如图,正方形ABCD的边长为4,点P,Q,R,S分别在AB,BC,CD,DA上,且BQ=2AP,CR=3AP,DS=4AP. 如图,AB是⊙O直径,∠AOC=130°,则∠D=
如图,AB是⊙O直径,∠AOC=130°,则∠D=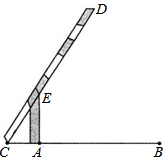 如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据:
如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据: 如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,∠C=∠D=135°,求∠A的度数.
如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,∠C=∠D=135°,求∠A的度数.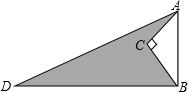 如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积=
如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积=