题目内容
12．
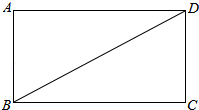如图，BD是矩形ABCD的一条对角线．（1）作BD的垂直平分线EF，分别交AD，BC于点E，F，垂足为点O（要求用尺规作图，保留作图痕迹，不要求写作法）；
（2）求证：DE=BF．
分析 （1）利用线段垂直平分线的作法得出直线EF即可；
（2）利用全等三角形的判定方法SAS得出△DEO≌△BFO进而求出即可．
解答 （1）解：如图所示：EF即为所求；
；
（2）证明：∵四边形ABCD为矩形，∴AD∥BC．
∴∠ADB=∠CBD．
∵EF垂直平分线段BD，∴BO=DO．
在△DEO和△BFO中，
∵$\left\{\begin{array}{l}{∠ADB=∠CBD}\\{DO=BO}\\{∠DOE=∠BOF}\end{array}\right.$，
∴△DEO≌△BFO（ASA），
∴DE=BF．
点评 此题主要考查了全等三角形的判定与性质以及线段垂直平分线的作法，正确掌握全等三角形的判定方法是解题关键．
练习册系列答案
相关题目
2．在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为“梦之点”，例如点（-1，-1），（0，0），（$\sqrt{2}，\sqrt{2}$），…都是“梦之点”，显然，这样的“梦之点”有无数个，应用：若点P（2，m）是反比例函数y=$\frac{n}{x}$（n为常数，n≠0）的图象上的“梦之点”，则这个反比例函数的解析式是（ ）
| A． | y=$\frac{2}{x}$ | B． | y=$\frac{2m}{x}$ | C． | y=$\frac{{m}^{2}}{x}$ | D． | y=$\frac{4}{x}$ |
3．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  等边三角形 | B． |  平行四边形 | C． |  正方形 | D． |  正五边形 |
17．⊙O的半径为5，同一平面内有一点P，且OP=7，则P与⊙O的位置关系是（ ）
| A． | P在圆内 | B． | P在圆上 | C． | P在圆外 | D． | 无法确定 |
4．
为了了解某市九年级学生的体育成绩（成绩均为整数），随机抽取了部分学生的体育成绩并分段（A：20.5～22.5；B：22.5～24.5；C：24.5～26.5；D：26.5～28.5；E：28.5～30.5）统计，得到统计图、表如下．
根据上面的信息，回答下列问题：
（1）统计表中，a=0.15，b=60，c=240；将统计图补充完整．
（2）小明说：“这组数据的众数一定在C中．”你认为小明的说法正确吗？错误（选填“正确”或“错误”）．
（3）若成绩在27分以上定为优秀，则该市48 000名九年级学生中体育成绩为优秀的学生人数约有多少？
为了了解某市九年级学生的体育成绩（成绩均为整数），随机抽取了部分学生的体育成绩并分段（A：20.5～22.5；B：22.5～24.5；C：24.5～26.5；D：26.5～28.5；E：28.5～30.5）统计，得到统计图、表如下．| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
（1）统计表中，a=0.15，b=60，c=240；将统计图补充完整．
（2）小明说：“这组数据的众数一定在C中．”你认为小明的说法正确吗？错误（选填“正确”或“错误”）．
（3）若成绩在27分以上定为优秀，则该市48 000名九年级学生中体育成绩为优秀的学生人数约有多少？
如图，四边形ABCD内接于⊙O，AD∥BC，P为BD上一点，∠APB=∠BAD．