题目内容
1.先化简,再求值:(x+2-$\frac{12}{x-2}$)÷$\frac{4-x}{x-2}$,其中x=2$\sqrt{2}$-4.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{{x}^{2}-4-12}{x-2}$•$\frac{x-2}{4-x}$
=-$\frac{(x+4)(x-4)}{x-2}$•$\frac{x-2}{x-4}$
=-x-4,
当x=2$\sqrt{2}$-4时,原式=-2$\sqrt{2}$+4-4=-2$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
11.截至2014年5月底,某市人口总数已达420000人.4520000用科学记数法表示为( )
| A. | 0.452×108 | B. | 4.52×107 | C. | 4.52×106 | D. | 4.52×105 |
9.两条对角线分别为6cm,8cm的菱形的周长是( )
| A. | 10cm | B. | 20cm | C. | 22cm | D. | 24cm |
16.下列运算正确的是( )
| A. | (a3)2=a5 | B. | ($\frac{1}{2}$a3b)2=$\frac{1}{4}$a6b2 | C. | (-x-y)2=x2-2xy+y2 | D. | (-a-b)(a+b)=a2-b2 |
6.如果a的倒数是-2,那么a等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
11.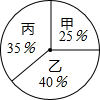 某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?
 某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?
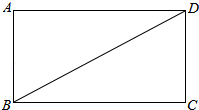 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线.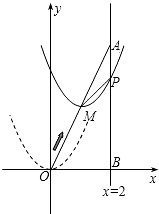 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.