题目内容
2.在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(-1,-1),(0,0),($\sqrt{2},\sqrt{2}$),…都是“梦之点”,显然,这样的“梦之点”有无数个,应用:若点P(2,m)是反比例函数y=$\frac{n}{x}$(n为常数,n≠0)的图象上的“梦之点”,则这个反比例函数的解析式是( )| A. | y=$\frac{2}{x}$ | B. | y=$\frac{2m}{x}$ | C. | y=$\frac{{m}^{2}}{x}$ | D. | y=$\frac{4}{x}$ |
分析 先由“梦之点”的定义得出m=2,再将点P坐标代入y=$\frac{n}{x}$,运用待定系数法即可求出反比例函数的解析式.
解答 解:(1)∵点P(2,m)是“梦之点”,
∴m=2,
∵点P(2,2)在反比例函数y=$\frac{n}{x}$(n为常数,n≠0)的图象上,
∴n=2×2=4,
∴反比例函数的解析式为y=$\frac{4}{x}$;
故选D.
点评 本题考查了待定系数法求反比例函数的解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
13.某厂共有120名生产工人,每个工人每天可生产螺栓50个或螺母20个,已知一个螺栓与两个螺母配成一套,设每天安排x名工人生产螺栓,y名工人生产螺母,才能使每天生产出来的产品配成最多套.则所列的方程组是( )
| A. | $\left\{\begin{array}{l}{x+y=120}\\{50x=20y×2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=120}\\{50x=20y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{50x+20y=120}\\{50x×2=20y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=120}\\{50x×2=20y}\end{array}\right.$ |
10.一次函数y=-2x-1的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.若方程x2+x-1=0的两实根为α、β,那么下列式子正确的是( )
| A. | α+β=1 | B. | αβ=1 | C. | α2+β2=2 | D. | $\frac{1}{α}$+$\frac{1}{β}$=1 |
11.截至2014年5月底,某市人口总数已达420000人.4520000用科学记数法表示为( )
| A. | 0.452×108 | B. | 4.52×107 | C. | 4.52×106 | D. | 4.52×105 |

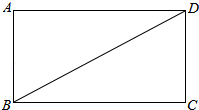 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线.