题目内容
7.某处山坡上有一棵与水平面垂直的大树,狂风过后,大树被刮的倾斜后折断,倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m.(1)求∠DAC的度数;
(2)这棵大树折断前高约多少米?(结果精确到个位,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
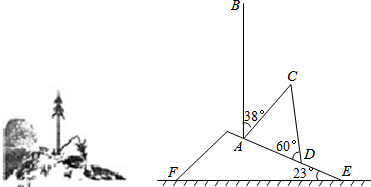
分析 (1)延长BA交EF于点G,在RT△AGE中,求得∠GAE=67°,然后根据∠CAE=180°-∠GAE-∠BAC即可求得;
(2)过点A作AH⊥CD,垂足为H,在△ADH中,根据余弦函数求得DH,进而根据正弦函数求得AH,在RT△ACH中,求得CH=AH=2$\sqrt{3}$,然后根据AB=AC+CD即可求得.
解答 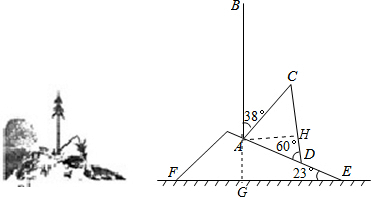 解:(1)延长BA交EF于点G,
解:(1)延长BA交EF于点G,
在RT△AGE中,∠E=23°,
∴∠GAE=67°,
又∠BAC=38°,
∴∠CAE=180°-67°-38°=75°.
(2)过点A作AH⊥CD,垂足为H,
在△ADH中,∠ADC=60°,AD=4,cos∠ADC=$\frac{DH}{AD}$,
∴DH=2,sin∠ADC=$\frac{AH}{AD}$,
∴AH=2$\sqrt{3}$.
在RT△ACH中,∠C=180°-75°-60°=45°,
∴AC=2$\sqrt{6}$,CH=AH=2$\sqrt{3}$.
∴AB=AC+CD=2$\sqrt{6}$+2$\sqrt{3}$+2≈10(米).
答:这棵大树折断前高约10米.
点评 本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | (a3)2=a5 | B. | ($\frac{1}{2}$a3b)2=$\frac{1}{4}$a6b2 | C. | (-x-y)2=x2-2xy+y2 | D. | (-a-b)(a+b)=a2-b2 |
17.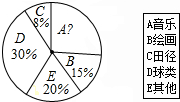 某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
“最喜欢的文体活动”调查统计表
(1)根据统计表和图中的信息将“统计表”填写完整;
(2)若该校共有初中学生900人,请你估计该校最喜欢“A音乐”的人数约有多少人?
 某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):“最喜欢的文体活动”调查统计表
| 项目 | A音乐 | B绘画 | C田径 | D球类 | E其他 |
| 频数 | 正正正正正正 | ||||
| 人数(人) | 20 |
(2)若该校共有初中学生900人,请你估计该校最喜欢“A音乐”的人数约有多少人?

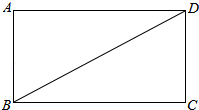 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线.