题目内容
6.化简求值:(1)($\frac{{x}^{2}}{x-1}+\frac{2x}{1-x}$)$÷\frac{x}{x-1}$,其中x=$\sqrt{3}+2$.
(2)已知x=2-$\sqrt{3}$,求代数式(7+4$\sqrt{3}$)x2+(2+$\sqrt{3}$)x+$\sqrt{3}$的值.
分析 (1)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可;
(2)先把二次根式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=$\frac{x(x-2)}{x-1}$•$\frac{x-1}{x}$
=x-2,
当x=$\sqrt{3}$+2时,原式=$\sqrt{3}$;
(2)原式=(2+$\sqrt{3}$)2x2+(2+$\sqrt{3}$)x+$\sqrt{3}$
=(2+$\sqrt{3}$)x[(2+$\sqrt{3}$)x+1]+$\sqrt{3}$,
当x=2-$\sqrt{3}$时,
原式=(2+$\sqrt{3}$)(2-$\sqrt{3}$)[(2+$\sqrt{3}$)(2-$\sqrt{3}$)+1]+$\sqrt{3}$
=(4-3)(4-3+1)+$\sqrt{3}$
=2+$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.小敏在百度中输入“雾霾”,能搜索到与之相关的结果各数约为77400000个,77400000用科学记数法表示为( )
| A. | 0.774×108 | B. | 7.74×107 | C. | 77.4×106 | D. | 7.74×108 |
14.已知点P(a,3)、Q(-2,b)关于y轴对称,则$\frac{a-b}{a+b}$=( )
| A. | -5 | B. | 5 | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
 如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
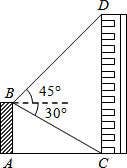 如图,某同学站在低楼AB上观察高楼CD,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,经过查找资料了解到楼房CD的高度为51.7m,求楼间距AC.($\sqrt{3}≈1.7$)
如图,某同学站在低楼AB上观察高楼CD,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,经过查找资料了解到楼房CD的高度为51.7m,求楼间距AC.($\sqrt{3}≈1.7$)