题目内容
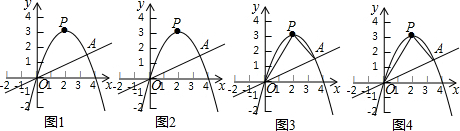
11.如图,二次函数y=-x2+4x与一次函数y=$\frac{1}{2}$x的图象相交于点A.(1)如图1,请用配方法求二次函数图象的最高点P的坐标;
(2)如图2,求点A的坐标;
(3)如图3,连结抛物线的最高点P与点O、A得到△POA,求△POA的面积;
(4)如图4,在抛物线上存在一点M(M与P不重合)使△MOA的面积等于△POA的面积,请求出点M的坐标.
分析 (1)用配方法配成顶点式;
(2)联立方程组求交点坐标;
(3)将不特殊图形用割补法求面积;
(4)利用同底等高的方法求出点的坐标.
解答 解:(1)由题意,y=-x2-4x=-(x-2)2-4,
∴二次函数图象的最高点P(2,4),
(2)∵二次函数y=-x2+4x与一次函数y=$\frac{1}{2}$x的图象相交于点A,
∴$\left\{\begin{array}{l}{y={-x}^{2}+4x}\\{y=\frac{1}{2}x}\end{array}\right.$
∴$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(舍)或$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=\frac{7}{4}}\end{array}\right.$,
∴点A的坐标为($\frac{7}{2}$,$\frac{7}{4}$),
(3)如图1,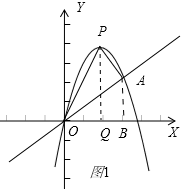
作⊥x轴于点Q,AB⊥x轴于点B,
∴S△POA=S△POQ+S梯形PQBA-S△AOB
=$\frac{1}{2}$×OQ×PQ+$\frac{1}{2}$(AB+PQ)×BQ-$\frac{1}{2}$×OB×AB
=$\frac{1}{2}$×2×4+$\frac{1}{2}$×($\frac{7}{4}$+4)×($\frac{7}{2}$-2)-$\frac{1}{2}$×$\frac{7}{2}×\frac{7}{4}$
=$\frac{21}{4}$;
(4)如图2,①点点M在直线OA上方时,
过P作OA的平行线,交抛物线于M,连接OM,AM,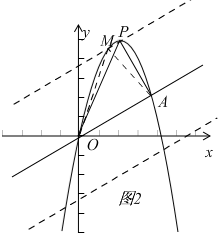
∴S△AOM=S△AOP;
设直线PM的解析式为y=$\frac{1}{2}$x+b,
∵P(2,4),
∴4=$\frac{1}{2}$×2+b,
∴b=3,
∴直线PM的解析式为y=$\frac{1}{2}$x+3①.
∵点M在抛物线y=-x2+4x②的图象上,
联立①②得,$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$(舍)或$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{15}{4}}\end{array}\right.$,
∴M($\frac{3}{2}$,$\frac{15}{4}$).
②由①知,直线PM的解析式为y=$\frac{1}{2}$x+3.
利用对称性得出另一条满足条件的直线解析式为y=$\frac{1}{2}$x-3③,
联立②③得,$\left\{\begin{array}{l}{x=\frac{7+\sqrt{97}}{4}}\\{y=\frac{-17+\sqrt{97}}{8}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{7-\sqrt{97}}{4}}\\{y=\frac{-17-\sqrt{97}}{8}}\end{array}\right.$,
∴M($\frac{7+\sqrt{97}}{4}$,$\frac{-17+\sqrt{97}}{8}$)或($\frac{7-\sqrt{97}}{4}$,$\frac{-17-\sqrt{97}}{8}$),
即:满足条件的点M的坐标为($\frac{3}{2}$,$\frac{15}{4}$).或($\frac{7+\sqrt{97}}{4}$,$\frac{-17+\sqrt{97}}{8}$)或($\frac{7-\sqrt{97}}{4}$,$\frac{-17-\sqrt{97}}{8}$).
点评 此题是二次函数的综合题,主要考查求图形的交点,用割补法求图形的面积等知识点,解本体的关键是割补法求不特殊图形的面积,难点是同底等高的三角形面积的运用.

 已知AC∥BD,∠CAE=30°,∠DBE=45°,求∠AEB的度数.
已知AC∥BD,∠CAE=30°,∠DBE=45°,求∠AEB的度数.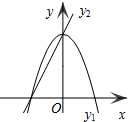 已知抛物线y1=-2x2+2和直线y2=2x+2的图象如图所示,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.则下列结论中一定成立的是②④(把所有正确结论的序号都填在横线上)
已知抛物线y1=-2x2+2和直线y2=2x+2的图象如图所示,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.则下列结论中一定成立的是②④(把所有正确结论的序号都填在横线上) 已知:如图,∠1与∠2互补,∠D=∠B,那么∠A=∠C,请说明理由.
已知:如图,∠1与∠2互补,∠D=∠B,那么∠A=∠C,请说明理由.