题目内容
16.一个边数为2n的多边形内所有对角线的条数是边数为n的多边形内所有对角线条数的6倍,求这两个多边形的边数.分析 根据多边形的对角线公式$\frac{1}{2}$n(n-3)进行计算即可得解.
解答 解:依题意有
$\frac{1}{2}$×2n(2n-3)=6×$\frac{1}{2}$n(n-3),
解得n=6,
2n=12.
故这两个多边形的边数是6,12.
点评 本题考查了多边形的对角线,熟记对角线公式是解题的关键.

练习册系列答案
相关题目
7.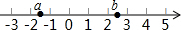 实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )
实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )
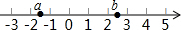 实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )
实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )| A. | 0 | B. | -2a | C. | 2b | D. | -2a+2b |
4.单项式-$\frac{2x{y}^{2}}{5}$的系数和次数分别是( )
| A. | $\frac{2}{5}$,3 | B. | -$\frac{2}{5}$,2 | C. | -2,3 | D. | -$\frac{2}{5}$,3 |
13.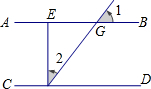 如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )
如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )
 如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )
如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )| A. | 54° | B. | 46° | C. | 44° | D. | 36° |
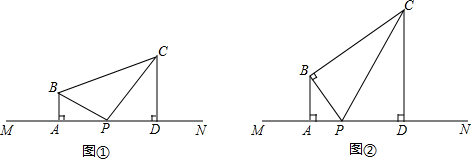
 在△ABC中,AB=AC,∠BAC=90°,若点D、E在边BC上,∠DAE=45°,BE=CD=4,求AC的长.
在△ABC中,AB=AC,∠BAC=90°,若点D、E在边BC上,∠DAE=45°,BE=CD=4,求AC的长. 如图,在△ABC中,AB=3,BC=6,△ABC的高AD和CE的比是多少?
如图,在△ABC中,AB=3,BC=6,△ABC的高AD和CE的比是多少?