题目内容
7．
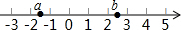实数a、b在数轴上的位置如图，则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{（a-b）^{2}}$的结果是（ ）| A． | 0 | B． | -2a | C． | 2b | D． | -2a+2b |
分析 先根据数轴确定a，b的范围，再根据二次根式的性质进行化简，即可解答．
解答 解：由数轴可得：a＜0＜b，|a|＜|b|，
$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{（a-b）^{2}}$
=|a|+|b|-|a-b|
=-a+b+a-b
=0．
故选：A．
点评 本题考查了实数与数轴，解决本题的关键是根据数轴确定a，b的范围．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
17．甲、乙两班学生参加植树造林，已知甲班每天比乙班少植3棵树，甲班植60棵树与乙班植80棵树所用天数相等．若设甲班每天植树x棵，则可列方程（ ）
| A． | $\frac{60}{x}=\frac{80}{x+3}$ | B． | $\frac{60}{x}=\frac{80}{x-3}$ | C． | $\frac{60}{x-3}=\frac{80}{x}$ | D． | $\frac{60}{x+3}=\frac{80}{x}$ |
2．
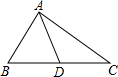如图，在Rt△ABC中，∠BAC=90°，AB=6，D是斜边BC的中点，若AD=5，则AC等于（ ）
如图，在Rt△ABC中，∠BAC=90°，AB=6，D是斜边BC的中点，若AD=5，则AC等于（ ）| A． | 8 | B． | 64 | C． | 5$\sqrt{2}$ | D． | 6$\sqrt{3}$ |
19．式子$\frac{\sqrt{2{x}^{2}+1}}{x-1}$有意义的x的取值范围是（ ）
| A． | x≥0且x≠1 | B． | x≠1 | C． | x≥-$\frac{1}{2}$ | D． | x≤0且x≠-1 |
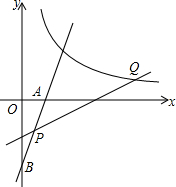如图，直线l：y=kx-2k交坐标轴于A，B两点，点P（m，n）为直线l上的一点，且满足关系式2m2+2n2-4m+8n+10=0．