题目内容
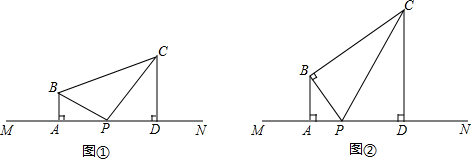
12.如图,AB⊥MN于A,CD⊥MN于D.点P是MN上一个动点.(1)如图①.BP平分∠ABC,CP平分∠BCD交BP于点P.若AB=4,CD=6.试求AD的长;
(2)如图②,∠BPC=∠BPA,BC⊥BP,若AB=4,求CD的长.
分析 (1)过点P作PE⊥BC于E,过点B作BF⊥CD于F,利用角平分线性质定理可得AP=PE,再由全等三角形的判定方法可知Rt△ABP≌Rt△EBP,同理可证Rt△CEP≌Rt△CDP,进而可得AB=BE,CE=CD,即BC=10,易证四边形ABFD是矩形,所以BF=AD,利用勾股定理求出BF的长即可;
(2)如图2,延长CB和PA,记交点为点Q.根据等腰△QPC“三合一”的性质证得QB=BC;由相似三角形(△QAB∽△QDC)的对应边成比例得到,则CD=2AB,问题得解;
解答 解:(1)过点P作PE⊥BC于E,过点B作BF⊥CD于F,
∵AB⊥MN于A,CD⊥MN于D,BP平分∠ABC,
∴AP=PE,
在Rt△ABP和Rt△EBP中,
$\left\{\begin{array}{l}{AP=EP}\\{BP=BP}\end{array}\right.$,
∴Rt△ABP≌Rt△EBP,
∴AB=BE=4,
同理可得CE=CD=6,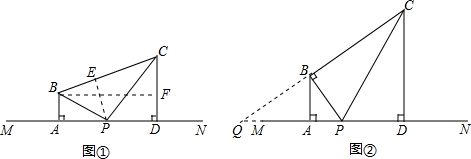
∴BC=BE+CE=10,
易证四边形ABFD是矩形,
∴BF=AD,CF=6-4=2,
∴AD=$\sqrt{B{C}^{2}-C{F}^{2}}$=4$\sqrt{6}$;
(2)延长CB和PA,记交点为点Q.
∵∠BPC=∠BPA,BC⊥BP,
∴QB=BC(等腰三角形“三合一”的性质).
∵BA⊥MN,CD⊥MN,
∴AB∥CD,
∴△QAB∽△QDC,
∴$\frac{AB}{CD}=\frac{QB}{QC}=\frac{1}{2}$,
∴CD=2AB=2×4=8.
点评 本题考查了勾股定理的运用、矩形的判定和性质、等腰三角形的判定和性质以及全等三角形的判定和性质、相似三角形的判定和性质,题目的综合性较强,难度较大,解题的关键是正确添加辅助线构造直角三角形.

| A. | x<-$\frac{3}{4}$ | B. | x>-$\frac{3}{4}$ | C. | x>$\frac{3}{4}$ | D. | x<$\frac{3}{4}$ |
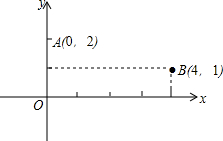 已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.
已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.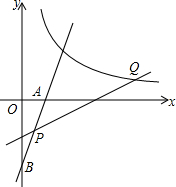 如图,直线l:y=kx-2k交坐标轴于A,B两点,点P(m,n)为直线l上的一点,且满足关系式2m2+2n2-4m+8n+10=0.
如图,直线l:y=kx-2k交坐标轴于A,B两点,点P(m,n)为直线l上的一点,且满足关系式2m2+2n2-4m+8n+10=0.