题目内容
17.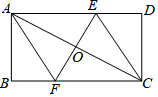 如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.(1)求证:四边形AFCE是菱形.
(2)若AC=8,EF=6,求BF的长.
分析 (1)由条件可先证四边形AFCE为平行四边形,再结合线段垂直平分线的性质可证得结论;
(2)由菱形的性质可求得AE=CF=5,设BF=x,在Rt△ABF和Rt△ABC中,分别利用勾股定理可得到关于x的方程,可求得BF的长.
解答 (1)证明:
∵O为AC中点,EF⊥AC,
∴EF为AC的垂直平分线,
∴EA=EC,FA=FC,
∴∠EAC=∠ECA,∠FAC=∠FCA.
∵AE∥CF,
∴∠EAC=∠FCA,
∴∠FAC=∠ECA,
∴AF∥CE,
∴四边形AFCE平行四边形.
又∵EA=EC,
∴平行四边形AFCE是菱形.
(2)∵四边形AFCE是菱形,AC=8,EF=6,
∴OE=3,OA=4,
∴AE=CF=5,
设BF=x,
在Rt△ABF中,AB2=AF2-BF2,在Rt△ABC中,AB2=AC2-BC2.
∴52-x2=82-(x+5)2,
解得$x=\frac{7}{5}$,
∴$BF=\frac{7}{5}$.
点评 本题主要考查菱形的判定和性质,掌握菱形的判定方法和菱形的性质是解题的关键,在求BF的长时,注意方程思想的应用.

练习册系列答案
相关题目
15.某物流公司规定:办理托运业务,当物品的重量不超过16千克时,需付基础费30元和保险费a元;当物品重量超过16千克时,除了付以上的基础费和保险费外,超过部分还需付每千克b元的超重费.右表是该公司最近承接托运的两包物品重量和所收取的费用.
试问在物品可拆分的情况下,托运55千克物品的最少费用是( )
| 物品重量(千克) | 收取费用(元) |
| 18 | 39 |
| 25 | 60 |
| A. | 120 | B. | 132 | C. | 135 | D. | 150 |
 如图,一段抛物线:y=-(x-1)2+1(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;如此进行下去,直至得到C8,若点P(14.5,m)在抛物线C8上,则m的值为-$\frac{3}{4}$.
如图,一段抛物线:y=-(x-1)2+1(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;如此进行下去,直至得到C8,若点P(14.5,m)在抛物线C8上,则m的值为-$\frac{3}{4}$.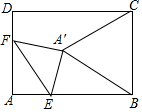 如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2$\sqrt{3}$,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为4或4$\sqrt{3}$.
如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2$\sqrt{3}$,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为4或4$\sqrt{3}$.
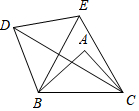 如图,将△ABC绕点B逆时针旋转60°得△DBE,连接CD,若AB=AC=5,BC=6,则CD=$4+3\sqrt{3}$.
如图,将△ABC绕点B逆时针旋转60°得△DBE,连接CD,若AB=AC=5,BC=6,则CD=$4+3\sqrt{3}$.