Question

1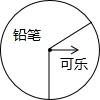．如图，某商场设立了一个可以自由转动的转盘，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．表是活动进行中的一组统计数据：
（1）计算并完成表格：

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”的次数m	68	111	136	345	564	701
落在“铅笔”的频率$\frac{m}{n}$	0.68	0.74	0.68	0.69	0.71	0.70

（2）请估计，当n很大时，频率将会接近多少？
（3）假如你去转动转盘一次，你获得可乐的概率是多少？

Answer 1

分析 （1）分别利用表格中数据结合频率公式求出即可；
（2）利用（1）中所求频率即可估计出当n很大时，频率将会接近的值；
（3）利用（2）中所求可得出落在“铅笔”的概率，进而得出落在“可乐”的概率．

解答 解：（1）填表如下：

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”的次数m	68	111	136	345	564	701
落在“铅笔”的频率$\frac{m}{n}$	0.68	0.74	0.68	0.69	0.71	0.70

（2）由表格中数据可得：当n很大时，频率将会接近0.70；

（3）由（2）得：当n很大时，频率将会接近0.70，即落在“铅笔”的概率为：0.7，
则转动转盘一次，获得可乐的概率是：0.30．

点评 此题主要考查了频率求法以及利用频率估计概率，正确理解频率与概率之间的关系是解题关键．