题目内容
13.直角三角形的面积为6,周长为12,则这个直角三角形的斜边长为5.分析 设直角三角形的两条直角边长分别为a、b,斜边长为c,则a+b+c=12,$\frac{1}{2}$ab=6,a2+b2=c2,由完全平方公式得出c的方程,解方程即可.
解答 解:设直角三角形的两条直角边长分别为a、b,斜边长为c,
则a+b+c=12,$\frac{1}{2}$ab=6,a2+b2=c2,
∴a+b=12-c,ab=12,
∴(a+b)2-2ab=c2,
即(12-c)2-2×12=c2,
解得:c=5,
故答案为:5.
点评 本题考查了勾股定理、完全平方公式;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
1.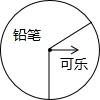 如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
(1)计算并完成表格:
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获得可乐的概率是多少?
 如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:(1)计算并完成表格:
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率$\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.71 | 0.70 |
(3)假如你去转动转盘一次,你获得可乐的概率是多少?
8.已知x2=9,|y|=8,且xy<0,则x+y的值等于( )
| A. | ±5 | B. | ±11 | C. | -5或11 | D. | -5或-11 |
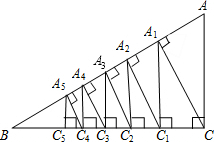 如图,在Rt△BCA中,∠C=90°,AC=3,BC=4,过点C作CA1⊥AB,垂足为点A1,再过点A1作A1C1⊥BC,垂足为点C1,…按以上的方法继续作下去,得到Rt△A5C5C4,求线段A5C5的长.
如图,在Rt△BCA中,∠C=90°,AC=3,BC=4,过点C作CA1⊥AB,垂足为点A1,再过点A1作A1C1⊥BC,垂足为点C1,…按以上的方法继续作下去,得到Rt△A5C5C4,求线段A5C5的长.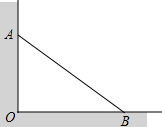 如图所示,在建筑工地上,为了支撑一堵墙,用一根5m的木材,顶端撑在墙上,底端撑在地面上,图中OB=4m.现在为了增加支撑的效果,底端先前移,顶端向上移,若移动距离相等,则应移动多少米?
如图所示,在建筑工地上,为了支撑一堵墙,用一根5m的木材,顶端撑在墙上,底端撑在地面上,图中OB=4m.现在为了增加支撑的效果,底端先前移,顶端向上移,若移动距离相等,则应移动多少米? 阅读下面的证明过程,在括号内填写适当的理由,并在横线上说明其中的因果关系.
阅读下面的证明过程,在括号内填写适当的理由,并在横线上说明其中的因果关系. 如图,已知△ABC中,∠C=90°,AB=t(t>0),∠A=α,∠B=β
如图,已知△ABC中,∠C=90°,AB=t(t>0),∠A=α,∠B=β