题目内容
11.观察下列各式:$\frac{1}{1×2}$=$\frac{1}{2}$=1-$\frac{1}{2}$;$\frac{1}{1×3}$=$\frac{1}{3}$=$\frac{1}{2}$×(1-$\frac{1}{3}$);$\frac{1}{1×4}$=$\frac{1}{4}$=$\frac{1}{3}$×(1-$\frac{1}{4}$);$\frac{1}{2×3}$=$\frac{1}{6}$=$\frac{1}{2}$-$\frac{1}{3}$;$\frac{1}{3×5}$=$\frac{1}{15}$=$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$);$\frac{1}{4×7}$=$\frac{1}{28}$=$\frac{1}{3}$×($\frac{1}{4}$-$\frac{1}{7}$);…
你能用类似的方法去写$\frac{1}{1×7}$和$\frac{1}{7×13}$吗?你会用含字母的式子表达发现的规律吗?
分析 由题意可知:分子是1,分母是两个数的乘积,分母的两个数相差几,就可以拆成几分之一乘以这两个数为分母,分子为1的两个分数的差,由此规律得出答案即可.
解答 解:$\frac{1}{1×7}$=$\frac{1}{6}$×(1-$\frac{1}{7}$),$\frac{1}{7×13}$=$\frac{1}{6}$×($\frac{1}{7}$-$\frac{1}{13}$),
设n、a为正整数,则$\frac{1}{n(n+a)}$=$\frac{1}{a}$×($\frac{1}{n}$-$\frac{1}{n+a}$).
点评 此题考查数字的变化规律,找出数字之间的运算规律,得出一般性的结论,进而解决问题.

练习册系列答案
相关题目
1.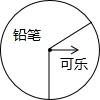 如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
(1)计算并完成表格:
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获得可乐的概率是多少?
 如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:(1)计算并完成表格:
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率$\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.71 | 0.70 |
(3)假如你去转动转盘一次,你获得可乐的概率是多少?
 阅读下面的证明过程,在括号内填写适当的理由,并在横线上说明其中的因果关系.
阅读下面的证明过程,在括号内填写适当的理由,并在横线上说明其中的因果关系. 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE交AD于点F,交AC于点E,若BE平分∠ABC,试判断△AEF的形状,并说明理由.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE交AD于点F,交AC于点E,若BE平分∠ABC,试判断△AEF的形状,并说明理由. 如图,已知△ABC中,∠C=90°,AB=t(t>0),∠A=α,∠B=β
如图,已知△ABC中,∠C=90°,AB=t(t>0),∠A=α,∠B=β