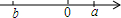题目内容

16．等腰三角形的顶角为70°，底边上的高为11.3，则腰长为（　　）
A．10.24B．16.14C．19.7D．13.79

分析 先画出几何图形，如图，AB=AC，高AD=11.3，∠BAC=70°，根据等腰三角形的性质得AD平分∠BAC，则∠BAD=$\frac{1}{2}$∠BAC=35°，然后在Rt△BAD中，利用∠BAD的余弦可求AB的长．

解答 解：如图，AB=AC，高AD=11.3，∠BAC=70°，
∵AD为等腰△ABC的高，
∴AD平分∠BAC，
∴∠BAD=$\frac{1}{2}$∠BAC=35°，
在Rt△BAD中，∵cos∠BAD=$\frac{AD}{AB}$，
∴AB=$\frac{11.3}{cos35°}$≈13.79．
故选D．

点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了等腰三角形的性质．

练习册系列答案
相关题目
6．如图，在直角△ABC中，∠C=90°，AC=4，BC=3，D是AC的中点，点E是AB边上的一动点，点F是射线BC上一动点，且∠FDE=90°，设AE=x，CF=y．
（1）当△ADE与△ABC相似时，求：AE的长．
（2）当点F在线段BC上时，求：y关于x的函数解析式及定义域．
（3）连结CE，若△CDE为等腰三角形，求BF的长．
7．一个分数，分子比分母小1，如果分子减去1，分母加上1，那么所得的分数等于$\frac{8}{9}$，试求这个分数．
4．如图所示，在建筑工地上，为了支撑一堵墙，用一根5m的木材，顶端撑在墙上，底端撑在地面上，图中OB=4m．现在为了增加支撑的效果，底端先前移，顶端向上移，若移动距离相等，则应移动多少米？
11．点A，B在数轴上分别表示有理数a，b（不妨设A点在B点左侧），A，B两点间的距离表示为|AB|，设点O表示原点，当A，B两点中有一点在原点时，不妨设点A在原点，如图（1），|AB|=|OB|=|b|，当A，B两点都不在原点时：
①如图（2），点A，B都在原点的右边，|AB|=|OB|-|OA|=|b|-|a|．
②如图（3），点A，B都在原点的左边，|AB|=|OA|-|OB|=|a|+|b|．
③如图（4），点A，B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|．

根据以上信息，回答下列问题．
（1）数轴上表示2和5的两点之间的距离是3．数轴上表示-2和-5的两点之间的距离是3．数轴上表示1和-3的两点之间的距离是4．数轴上有表示x的点A和表示-1的点B，如果|AB|=2，那么x为-3或1．
（2）有理数a，b在数轴上对应的位置如图所示，试化简：|a-b|+|a+b|+|a|-|b|．
1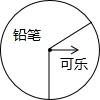．如图，某商场设立了一个可以自由转动的转盘，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．表是活动进行中的一组统计数据：
（1）计算并完成表格：
转动转盘的次数n1001502005008001000
落在“铅笔”的次数m68111136345564701
落在“铅笔”的频率$\frac{m}{n}$0.680.740.680.690.710.70
（2）请估计，当n很大时，频率将会接近多少？
（3）假如你去转动转盘一次，你获得可乐的概率是多少？
8．已知x2=9，|y|=8，且xy＜0，则x+y的值等于（　　）
A．±5B．±11C．-5或11D．-5或-11
5．分别写出一个符合下列条件的算式：
（1）三个加数都是负整数，和为-10；
（2）三个加数中有一个加数是0，和为-10；
（3）三个加数中有一个加数是负整数，而另外两个加数是正整数，和是-10；
（4）三个加数中两个加数是负整数，另一个加数是正整数，和是-10．
6．已知|x|=1，|y|=2，|z|=3，且xy＜0，xyz＞0，求（x+y+z）•（xy+yz）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网