题目内容
11.已知a2=9,|b|=4,ab<0,a+b>0,求(2a+b)2+ab的值.分析 根据有理数的乘方,绝对值的性质求出a、b的值,再判断出ab的对应情况,然后代入代数式进行计算即可得解.
解答 解:∵a2=9,|b|=4,
∴a=±3,b=±4,
∵ab<0,a+b>0,
∴a=3,b=-4,
∴(2a+b)2+ab=(2×3-4)2+3×(-4)=4-12=-8.
点评 本题考查了代数式求值,绝对值的性质,有理数的乘方,熟记性质与概念并确定出a、b的值是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
1.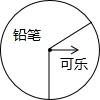 如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
(1)计算并完成表格:
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获得可乐的概率是多少?
 如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:(1)计算并完成表格:
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率$\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.71 | 0.70 |
(3)假如你去转动转盘一次,你获得可乐的概率是多少?
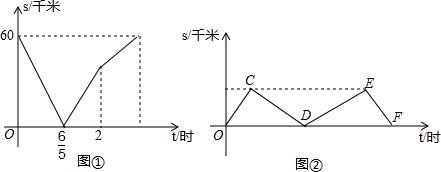
 解不等式组:$\left\{\begin{array}{l}{3x-1<2(x+1)①}\\{\frac{x+3}{2}≥1②}\end{array}\right.$,并在所给的数轴上表示出其解集.
解不等式组:$\left\{\begin{array}{l}{3x-1<2(x+1)①}\\{\frac{x+3}{2}≥1②}\end{array}\right.$,并在所给的数轴上表示出其解集.
 如图,在直角△ABC中,∠C=90°,AC=4,BC=3,D是AC的中点,点E是AB边上的一动点,点F是射线BC上一动点,且∠FDE=90°,设AE=x,CF=y.
如图,在直角△ABC中,∠C=90°,AC=4,BC=3,D是AC的中点,点E是AB边上的一动点,点F是射线BC上一动点,且∠FDE=90°,设AE=x,CF=y.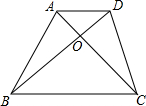 如图,梯形ABCD中,AD∥BC,对角线AC,BD交于点O,已知$\frac{AD}{BC}$=$\frac{2}{3}$,S△ACD=2,那么梯形ABCD的面积=5.
如图,梯形ABCD中,AD∥BC,对角线AC,BD交于点O,已知$\frac{AD}{BC}$=$\frac{2}{3}$,S△ACD=2,那么梯形ABCD的面积=5.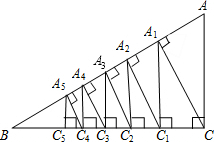 如图,在Rt△BCA中,∠C=90°,AC=3,BC=4,过点C作CA1⊥AB,垂足为点A1,再过点A1作A1C1⊥BC,垂足为点C1,…按以上的方法继续作下去,得到Rt△A5C5C4,求线段A5C5的长.
如图,在Rt△BCA中,∠C=90°,AC=3,BC=4,过点C作CA1⊥AB,垂足为点A1,再过点A1作A1C1⊥BC,垂足为点C1,…按以上的方法继续作下去,得到Rt△A5C5C4,求线段A5C5的长. 如图,AB∥CD,FG平分∠EFD,∠1=80°,则∠2=40°.
如图,AB∥CD,FG平分∠EFD,∠1=80°,则∠2=40°.