题目内容
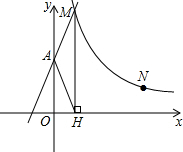 如图,直线y=2x+2与y轴交于A点,与反比例函数y=
如图,直线y=2x+2与y轴交于A点,与反比例函数y=| k |
| x |
(1)求k的值;
(2)点N(a,1)是反比例函y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先由直线y=2x+2与y轴交于A点,求出A点坐标为(0,2),OA=2,根据OA=2OH,得出OH=1.由MH⊥x轴可知M点横坐标为1,而点M在直线y=2x+2上,所以当x=1时,y=2×1+2=4,即M(1,4),再将点M的坐标代入y=
,即可求出k的值;
(2)先由点N(a,1)是反比例函y=
(x>0)图象上的点,求出a=4,即点N(4,1).再作N关于x轴的对称点N′,连结MN′,交x轴于点P,此时PM+PN最小.根据关于x轴对称的两点的坐标特征得出点N′(4,-1),利用待定系数法求出直线MN′的解析式,再令y=0,求出x的值,进而得到点P的坐标.
| k |
| x |
(2)先由点N(a,1)是反比例函y=
| 4 |
| x |
解答:解:(1)∵直线y=2x+2与y轴交于A点,
∴A点坐标为(0,2),OA=2,
∵OA=2OH,
∴OH=1.
∵MH⊥x轴,
∴M点横坐标为1,
∵点M在直线y=2x+2上,
∴当x=1时,y=2×1+2=4,
∴M(1,4),
∵点M在反比例函数y=
(x>0)的图象上,
∴k=1×4=4;
(2)存在.
∵点N(a,1)是反比例函y=
(x>0)图象上的点,
∴a=4,即点N(4,1).
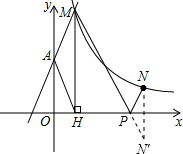 作N关于x轴的对称点N′,连结MN′,交x轴于点P,此时PM+PN最小.
作N关于x轴的对称点N′,连结MN′,交x轴于点P,此时PM+PN最小.
∵N与N′关于x轴,点N(4,1),
∴点N′(4,-1).
设直线MN′的解析式为y=mx+n,
则
,解得
,
∴直线MN′的解析式为y=-
x+
,
令y=0,得x=
,
∴点P的坐标为(
,0).
∴A点坐标为(0,2),OA=2,
∵OA=2OH,
∴OH=1.
∵MH⊥x轴,
∴M点横坐标为1,
∵点M在直线y=2x+2上,
∴当x=1时,y=2×1+2=4,
∴M(1,4),
∵点M在反比例函数y=
| k |
| x |
∴k=1×4=4;
(2)存在.
∵点N(a,1)是反比例函y=
| 4 |
| x |
∴a=4,即点N(4,1).
 作N关于x轴的对称点N′,连结MN′,交x轴于点P,此时PM+PN最小.
作N关于x轴的对称点N′,连结MN′,交x轴于点P,此时PM+PN最小.∵N与N′关于x轴,点N(4,1),
∴点N′(4,-1).
设直线MN′的解析式为y=mx+n,
则
|
|
∴直线MN′的解析式为y=-
| 5 |
| 3 |
| 17 |
| 3 |
令y=0,得x=
| 17 |
| 5 |
∴点P的坐标为(
| 17 |
| 5 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及轴对称的性质.

练习册系列答案
相关题目
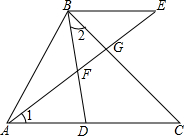 如图,D是AC上一点,BE∥AC,AE分别交BD,BC于点F,G.若∠1=∠2,线段BF,FG,FE之间有怎样的关系?请说明理由.
如图,D是AC上一点,BE∥AC,AE分别交BD,BC于点F,G.若∠1=∠2,线段BF,FG,FE之间有怎样的关系?请说明理由. 如图,△ABC中,BD⊥AC于D,CE⊥AB于E,AB=AC.求证:BE=CD.
如图,△ABC中,BD⊥AC于D,CE⊥AB于E,AB=AC.求证:BE=CD. 如图,长方形内有两个四分之一圆.
如图,长方形内有两个四分之一圆.