题目内容
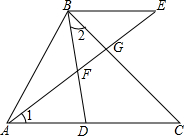 如图,D是AC上一点,BE∥AC,AE分别交BD,BC于点F,G.若∠1=∠2,线段BF,FG,FE之间有怎样的关系?请说明理由.
如图,D是AC上一点,BE∥AC,AE分别交BD,BC于点F,G.若∠1=∠2,线段BF,FG,FE之间有怎样的关系?请说明理由.考点:相似三角形的判定与性质
专题:
分析:利用平行和已知条件可得∠FBE=∠BGF,且∠BFE=∠GFB,可证明△BFG∽△EFB,可得到BF、FG、FE之间的关系.
解答:解:BF2=FG•FE,理由如下:
∵BE∥AC,
∴∠1=∠E,∠EBG=∠C,
∵∠DBE=∠2+∠EBG,∠BGF=∠1+∠C,且∠1=∠2,
∴∠FBE=∠BGF,且∠BFE=∠GFB,
∴△BFG∽△EFB,
∴
=
,
∴BF2=FG•EF.
∵BE∥AC,
∴∠1=∠E,∠EBG=∠C,
∵∠DBE=∠2+∠EBG,∠BGF=∠1+∠C,且∠1=∠2,
∴∠FBE=∠BGF,且∠BFE=∠GFB,
∴△BFG∽△EFB,
∴
| BF |
| EF |
| GF |
| BF |
∴BF2=FG•EF.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的对应边成比例是解题的关键.

练习册系列答案
相关题目
已知m为有理数,则整式m2(m2-1)-m2+1的值( )
| A、不是负数 | B、恒为负数 |
| C、恒为正数 | D、不等于0 |
 如图,在平行四边形ABCD中,E是BC上的3等分点,AE交BD于点F.
如图,在平行四边形ABCD中,E是BC上的3等分点,AE交BD于点F.
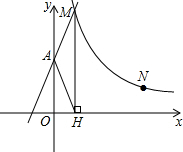 如图,直线y=2x+2与y轴交于A点,与反比例函数y=
如图,直线y=2x+2与y轴交于A点,与反比例函数y=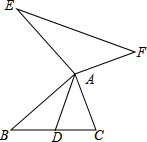 已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明.
已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明. 如图所示,长方形的宽是
如图所示,长方形的宽是