题目内容
19．无论x、y取任何值，多项式x2+y2-2x-4y+6的值总是（ ）| A． | 正数 | B． | 负数 | C． | 非负数 | D． | 无法确定 |
分析 利用完全平方公式把多项式分组配方变形后，利用非负数的性质判断即可．
解答 解：∵x2+y2-2x-4y+6=（x2-2x+1）+（y2-4y+4）+1=（x-1）2+（y-2）2+1≥1＞0，
∴多项式的值总是正数．
故选：A．
点评 此题考查了配方法的应用，以及非负数的性质，利用完全平方公式分组分解是解决问题的关键．
练习册系列答案
相关题目
10．下列各图中，∠1与∠2是对顶角的是（ ）
| A． |  | B． |  | C． |  | D． |  |
14．已知a2-2a-1=0，则a4-2a3-2a+1等于（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
11．钓鱼岛自古以来是中国的领土，岛屿周围的海域面积约170000平方公里，这里的“170000”用科学记数法表示为（ ）
| A． | 1.7×104 | B． | 17×104 | C． | 0.17×106 | D． | 1.7×105 |
8．使（x2+px+8）（x2-3x+q）乘积中不含x2和x3项的p，q的值分别是（ ）
| A． | p=3，q=1 | B． | p=-3，q=-9 | C． | p=0，q=0 | D． | p=-3，q=1 |
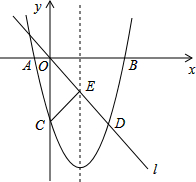如图，在平面直角坐标系中，已知抛物线y=ax2+bx-8与x轴交于A，B两点，与y轴交于点C，直线L经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为（-2，0），（6，-8）．