题目内容
12.解方程:$\frac{x-4}{{{x^2}+2x}}+\frac{2}{{{x^2}-4}}=\frac{1}{{{x^2}-2x}}$.分析 首先去掉分母,然后解整式方程,最后验根即可求解.
解答 解:∵$\frac{x-4}{{{x^2}+2x}}+\frac{2}{{{x^2}-4}}=\frac{1}{{{x^2}-2x}}$,
∴(x-2)(x-4)+2x=x+2,
∴x2-6x+8+2x=x+2,
x2-5x+6=0,
(x-2)(x-3)=0,
解得x1=2,x2=3,
检验:当x1=2时,x(x-2)(x+2)=0,是增根;
当x2=3时,x(x-2)(x+2)=15≠0,
∴x=3是原方程的解.
点评 此题主要考查了解分式方程,其中(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.

练习册系列答案
相关题目
3.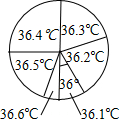 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )| 体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
| 人数(人) | 4 | 8 | 8 | 10 | x | 2 |
| A. | 这些体温的众数是8 | B. | 这些体温的中位数是36.35 | ||
| C. | 这个班有40名学生 | D. | x=8 |
16.已知n是使$\sqrt{27n}$的值为整数的最小正整数,估算$\sqrt{n}$的值,下列说法正确的是( )
| A. | 在1和2之间 | B. | 在2和3之间 | C. | 在3和4之间 | D. | 在4和5之间 |
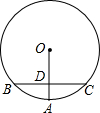 如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.
如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.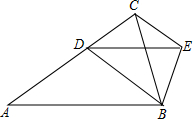 如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;
如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;