题目内容
17.(1)计算:2-1+(2π-1)0-$\frac{\sqrt{2}}{2}$-sin45°-$\sqrt{3}$tan30°(2)解方程:x2+4x-1=0.
分析 (1)根据实数的混合运算顺序和法则计算即可得;
(2)公式法求解可得.
解答 解:(1)原式=$\frac{1}{2}$+1-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$-$\sqrt{3}$×$\frac{\sqrt{3}}{3}$
=$\frac{1}{2}$+1-$\sqrt{2}$-1
=$\frac{1}{2}$-$\sqrt{2}$;
(2)∵a=1,b=4,c=-1,
∴△=16-4×1×(-1)=20>0,
则x=$\frac{-4±2\sqrt{5}}{2}$=-2$±\sqrt{5}$.
点评 本题主要考查解一元二次方程的能力和实数的混合运算,熟练掌握实数的混合运算顺序和法则及解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
8.我们把大于1的正整数m的三次幂按一定的规则“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3按此规则“分裂”后,最后一个奇数是341,则m的值为( )
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
5.如果$\sqrt{m+n}$=3,那么(m+n)2等于( )
| A. | 3 | B. | 9 | C. | 27 | D. | 81 |
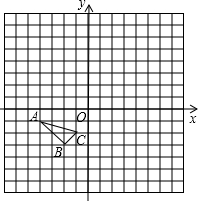 如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形).图中△ABC是格点三角形,点A,B,C的坐标分别是(-4,-1),(-2,-3),(-1,-2).
如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形).图中△ABC是格点三角形,点A,B,C的坐标分别是(-4,-1),(-2,-3),(-1,-2).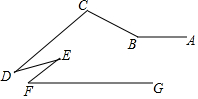 已知:如图,已知CD∥EF,∠C+∠F=∠ABC,若∠F=a°,a为关于x的一元一次方程$\frac{x-12}{3}$=-$\frac{x-15}{6}$+16的解
已知:如图,已知CD∥EF,∠C+∠F=∠ABC,若∠F=a°,a为关于x的一元一次方程$\frac{x-12}{3}$=-$\frac{x-15}{6}$+16的解



 如图,正方形ABCD的边长为1,E是边AB上一点,且AE=$\frac{1}{3}$,点F在边BC上,且BF=$\frac{1}{3}$,一束光线从点E射入到点F,若光线每碰到正方形的边时都会发生镜面反射.反射时反射角等于入射角,当光线再次经过点E时,光线发生反射的次数可能为( )
如图,正方形ABCD的边长为1,E是边AB上一点,且AE=$\frac{1}{3}$,点F在边BC上,且BF=$\frac{1}{3}$,一束光线从点E射入到点F,若光线每碰到正方形的边时都会发生镜面反射.反射时反射角等于入射角,当光线再次经过点E时,光线发生反射的次数可能为( )