题目内容
6.已知直线:y=-x+6交x轴、y轴于A、B两点,点C、M分别在OA、AB上且OC=2CA,AM=2MB,连接MC,将△ACM绕点M旋转180°.(1)记点C的对应点是点E,且点E在y轴上,求点E的坐标;
(2)求sin∠AMC的值.
分析 (1)根据题意画出图形,由直线解析式y=-x+6得点A、B的坐标,即可知OA=OB=6,从而得知∠OAB=∠OBA=45°、AB=6$\sqrt{2}$,由OC=2CA、AM=2MB得AC=2、AM=4$\sqrt{2}$、BM=2$\sqrt{2}$,根据旋转的性质知AC=FE=2、∠MFE=∠MAC=45°,结合∠FBE=∠OBA=45°可得∠MFE=∠FBE=45°,从而知BE=FE=2,即可得出答案;
(2)作CN⊥AM于点N,由AC=2、∠OAB=45°得CN=AN=ACcos∠OAB=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$、MN=AM-AN=3$\sqrt{2}$,根据勾股定理知MC=$\sqrt{C{N}^{2}+M{N}^{2}}$=2$\sqrt{5}$,在Rt△MCN中,根据sin∠AMC=$\frac{CN}{CM}$可得答案.
解答 解:(1)如图所示,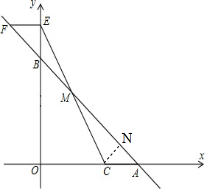
y=-x+6中,当x=0时y=6,即点B(0,6),
当y=0时-x+6=0,解得x=6,即点A(6,0),
则OA=OB=6,
∴∠OAB=∠OBA=45°,AB=6$\sqrt{2}$,
∵OC=2CA,AM=2MB,
∴AC=2,AM=4$\sqrt{2}$、BM=2$\sqrt{2}$,
∵将△ACM绕点M旋转180°得△FEM,
∴AC=FE=2,∠MFE=∠MAC=45°,
∵∠FBE=∠OBA=45°,
∴∠MFE=∠FBE=45°,
∴BE=FE=2,
则点E的坐标为(8,0);
(2)作CN⊥AM于点N,
∵AC=2,∠OAB=45°,
∴CN=AN=ACcos∠OAB=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
则MN=AM-AN=3$\sqrt{2}$,
∴MC=$\sqrt{C{N}^{2}+M{N}^{2}}$=2$\sqrt{5}$,
∴在Rt△MCN中,sin∠AMC=$\frac{CN}{CM}$=$\frac{\sqrt{2}}{2\sqrt{5}}$=$\frac{\sqrt{10}}{10}$.
点评 本题主要考查坐标与图形的变化-旋转、一次函数图象与坐标轴的交点、解直角三角形,根据题意及旋转的性质画出图形,并熟练掌握旋转的性质和解直角三角形的能力是解题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| 每回投球次数 | 30 | 60 | 90 | 150 | 200 | 300 | 400 | 500 |
| 每回进球次数 | 27 | 45 | 78 | 118 | 161 | 239 | 322 | 401 |
| 进球频率 | 0.900 | 0.750 | 0.867 | 0.787 | 0.805 | 0.797 | 0.805 | 0.802 |
(2)在比赛中该运动员因对手犯规获罚投篮一次,你能估计这次他能罚中的概率是多少吗?
| A. | 1cm 2cm 3cm | B. | 2cm 3cm 4cm | ||
| C. | 1cm 2cm 3.5cm | D. | 2cm 2cm 4cm |
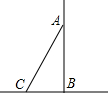 如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.
如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.
 如图,∠1=118°,∠2=62°,则a与b的位置关系是a∥b.
如图,∠1=118°,∠2=62°,则a与b的位置关系是a∥b.