题目内容
7.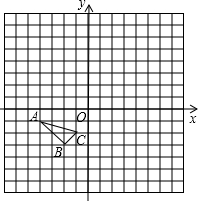 如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形).图中△ABC是格点三角形,点A,B,C的坐标分别是(-4,-1),(-2,-3),(-1,-2).
如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形).图中△ABC是格点三角形,点A,B,C的坐标分别是(-4,-1),(-2,-3),(-1,-2).(1)以O为旋转中心,把△ABC绕O点顺时针旋转90°后得到△A1B1C1,画出△A1B1C1;
(2)以O为位似中心,在第一象限内把△ABC放大2倍后得到△A2B2C2,画出△2B2C2;
(3)△ABC内有一点P(a,b),写出经过(2)位似变换后P的对应点P1的坐标.
分析 (1)利用网格特点和旋转的性质画出点A1、B1、C1,从而得到△A1B1C1;
(2)把点A、B、C的横纵坐标都乘以-2得到点A2、B2、C2的坐标,然后描点即可得到△2B2C2;
(3)利用(2)的对应点的坐标特点求解.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△2B2C2为所作;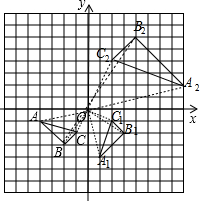
(3)点P的对应点P1的坐标为(-2a,-2b).
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了旋转变换.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.已知二次函数y=x2+bx+c的图象经过点(-1,-2),则bc有( )
| A. | 最小值-$\frac{1}{4}$ | B. | 最小值-$\frac{9}{4}$ | C. | 最大值$\frac{1}{4}$ | D. | 最大值$\frac{9}{4}$ |
19.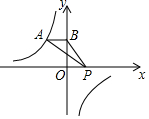 如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
 如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
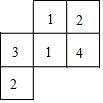 一个几何体由若干个相同的小立方体组成,如图是从上面看该几何体得到的形状图,小正方形中的数字表示在该位置小立方体的个数,请画出从正面和从左面看到的这个几何体的形状图.
一个几何体由若干个相同的小立方体组成,如图是从上面看该几何体得到的形状图,小正方形中的数字表示在该位置小立方体的个数,请画出从正面和从左面看到的这个几何体的形状图. 下面的框图表示解方程3x-7(x-1)=3-2(x+3)的流程,其中A代表的步骤是移项,步骤A对方程进行变形的依据是等式的基本性质1.
下面的框图表示解方程3x-7(x-1)=3-2(x+3)的流程,其中A代表的步骤是移项,步骤A对方程进行变形的依据是等式的基本性质1.
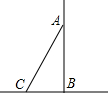 如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.
如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.