题目内容
5．
如图，点A和点B都在反比例函数y=$\frac{6}{x}$的图象上，且线段AB过原点，过点A作x轴的垂线段，垂足为C，P是线段OB上的动点，连接CP．设△ACP的面积为S，则下列说法正确的是（ ）| A． | S＞3 | B． | S＞6 | C． | 3≤S≤6 | D． | 3＜S≤6 |
分析 先作出△APC的高线PD，发现动点P组成的△APC中边AC为定值，因此S的确定取决于高线PD的长，设A（x，y），则B与A关于原点对称，根据面积求取值即可．
解答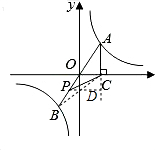 
解：过P作PD⊥AC于D，连接CB，
设A（x，y），则B（-x，-y），
∵点A在反比例函数y=$\frac{6}{x}$的图象上，
∴xy=6，
∵P是线段OB上的动点，
∴x≤PD≤2x，
∵S=S△APC=$\frac{1}{2}$AC•PD，
当PD最小时，此时P与O重合，PD=x，
∴S=S△APC=$\frac{1}{2}$xy=$\frac{1}{2}$×6=3，
当PD最大时，此时P与B重合，PD=2x，
∴S=S△APC=$\frac{1}{2}$AC•PD=$\frac{1}{2}$•y•2x=xy=6，
∴3≤S≤6，
故选C．
点评 本题考查了反比例函数系数k的几何意义，在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|，且保持不变．
练习册系列答案
相关题目
15．下列计算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | $\sqrt{9}+\sqrt{4}=\sqrt{5}$ | C． | $\sqrt{8}+\sqrt{2}=3\sqrt{2}$ | D． | $\sqrt{{{（{-5}）}^2}}=-5$ |
16．已知等腰三角形的周长为8，其中一边长为2，则另两边长为（ ）
| A． | 3，3 | B． | 2，4或3，3 | C． | 2，4 | D． | 2，3 |
20．不等式组$\left\{\begin{array}{l}{x-\frac{1}{2}＞0}\\{1-2x≤3}\end{array}\right.$的解集为（ ）
| A． | x$＞\frac{1}{2}$ | B． | x＜-1 | C． | -1＜x＜$\frac{1}{2}$ | D． | x$＞\frac{1}{2}$ |
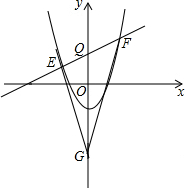如图，抛物线y=$\frac{1}{2}$x2-2交y轴于C，不平行于x轴的直线y=kx+3交抛物线于E、F，交y轴于点Q，在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG，若存在，请求出G点坐标；若不存在．请说明理由．
如图，天平右盘中的每个砝码的质量都是1克，则物体A的质量m（克）的取值范围，在数轴上可表示为（ ）
如图，在梯形ABCD中，AD∥BC，AB=CD，AC与BD相交于点E，∠ADB=60°，且BD：ED=3：1，BD=12，求梯形ABCD的周长．