已知等腰三角形的周长为8.其中一边长为2.则另两边长为( )A．3.3B．2.4或3.3C．2.4D．2.3 题目和参考答案——青夏教育精英家教网—

题目内容

16．已知等腰三角形的周长为8，其中一边长为2，则另两边长为（　　）

A．

3，3

B．

2，4或3，3

C．

2，4

D．

2，3

分析由于已知长度的边没有指明是等腰三角形的底边还是腰，因此要分类讨论，最后要根据三角形三边关系定理判断求出的结果是否符合题意．

解答解：①当等腰三角形的底长为2时，腰长=（8-2）÷2=3；
则等腰三角形的三边长为2、3、3；2+3＞3，能构成三角形．
②当等腰三角形的腰长为2时，底长=8-2×2=4；
则等腰三角形的三边长为4、2、2；2+2=4，不能构成三角形．
故等腰三角形另外两边的长为3，3．
故选：A．

点评本题考查了等腰三角形的性质及三角形的三边关系；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．

练习册系列答案

7．某商场服装部为了调动营业员的积极性，决定实行目标管理．为了确定一个适当的月销售日标，服装部统计了每位营业员在某月的销售额（单位：万元），数据如下：

销售额/万元	14	15	17	19	27	30
人数	1	6	3	4	5	1

（1）分别求出所有营业员月销售额的众数、中位数和平均数；
（2）如果想让一半左右的营业员有信心达到销售目标．月销售目标定为多少合适？

4．

如图，△ABC中AB的垂直平分线交AC于点D，已知∠ABC=∠ACB，AB=9，△BCD的周长等于11，则BC的长是2．

1．随机投掷一枚均匀的硬币，前9次都是正面朝上，第10次投掷时，（　　）

	A．	正面朝上的概率大		B．	反面朝上的概率大
	C．	正面朝上和反面朝上的概率一样大		D．	一定是反面朝上

8．下面是按一定规律排列且形式相似的一列数：
第1个数：a₁=$\frac{1}{2}$-（1+$\frac{-1}{2}$）；
第2个数：a₂=$\frac{1}{2}$-（1+$\frac{-1}{2}$）[1+$\frac{（-1）^{2}}{3}$][1+$\frac{（-1）^{3}}{4}$]
第3个数：a₃=$\frac{1}{2}$-（1+$\frac{-1}{2}$）[1+$\frac{（-1）^{2}}{3}$][1+$\frac{（-1）^{3}}{4}$][1+$\frac{（-1）^{4}}{5}$[1+$\frac{（-1）^{5}}{6}$]
（1）计算这三个数的结果（直接写答案）：
a₁=0；a₂=0；a₃=0；
（2）请按上述规律写出第4个数a₄的形式并计算结果；
（3）请根据上述规律写出第n （n为正整数）个数a_n的形式（中间部分用省略号，两端部分必须写详细），然后直接写出计算结果．

5．

如图，点A和点B都在反比例函数y=$\frac{6}{x}$的图象上，且线段AB过原点，过点A作x轴的垂线段，垂足为C，P是线段OB上的动点，连接CP．设△ACP的面积为S，则下列说法正确的是（　　）

6．

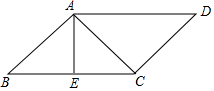在?ABCD中，AC⊥CD，AE⊥BC．
（1）∠EAC=55°，求∠D的度数；
（2）若AC=8，CD=6，求AE的长．

试题分类