题目内容
17. 如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 连接CO并延长交⊙O于D,则CD=10,根据圆周角定理可得:∠A=∠D,∠DBC=90°,又根据勾股定理可求得BD的长,继而求得答案.
解答  解:连接CO并延长交⊙O于D,则CD=10,
解:连接CO并延长交⊙O于D,则CD=10,
∵CD是直径,
∴∠DBC=90°,
∵DC=10,BC=8,
∴BD=$\sqrt{D{C}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴tan∠D=$\frac{BC}{BD}$=$\frac{8}{6}$=$\frac{4}{3}$,
∵∠A=∠D,
∴∠A的正切值等于$\frac{4}{3}$;
故选D.
点评 此题考查了圆周角定理、勾股定理以及三角函数.注意掌握辅助线的作法.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
13.观察下列关于x的单项式,探究其规律:
x,3x2,5x3,7x4,9x5,11x6,…
按照上述规律,第2015个单项式是( )
x,3x2,5x3,7x4,9x5,11x6,…
按照上述规律,第2015个单项式是( )
| A. | 2015x2015 | B. | 4029x2014 | C. | 4029x2015 | D. | 4031x2015 |
14.下列运算结果为a6的是( )
| A. | a2+a3 | B. | a2•a3 | C. | (-a2)3 | D. | a8÷a2 |
7.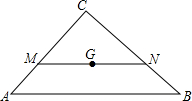 已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )
已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )
 已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )
已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )| A. | 3 | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
 如图,如果AB∥CD,∠B=35°,∠D=35°,那么BC与DE平行吗?为什么?
如图,如果AB∥CD,∠B=35°,∠D=35°,那么BC与DE平行吗?为什么? 观察如图,对照图象,请回答下列问题:
观察如图,对照图象,请回答下列问题: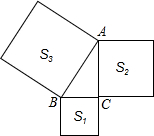 如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=6,S3=18,则S2=12.
如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=6,S3=18,则S2=12.