题目内容
9. 观察如图,对照图象,请回答下列问题:
观察如图,对照图象,请回答下列问题:(1)当x取何值时,2x-5=-x+1?
(2)当x取何值时,2x-5>-x+1?
(3)当x取何值时,2x-5<-x+1?
分析 (1)直线y=2x-5与直线y=-x+1的交点横坐标的值即为方程2x-5=-x+1的解;
(2)直线y=2x-5在直线y=-x+1上方的部分对应的x的取值范围即为不等式2x-5>-x+1的解集;
(3)直线y=2x-5在直线y=-x+1下方的部分对应的x的取值范围即为不等式2x-5<-x+1的解集.
解答 解:(1)由图象可知,直线y=2x-5与直线y=-x+1的交点的横坐标是2,所以当x取2时,2x-5=-x+1;
(2)由图象可知,当x>2时,直线y=2x-5落在直线y=-x+1的上方,即2x-5>-x+1;
(3)由图象可知,当x<2时,直线y=2x-5落在直线y=-x+1的下方,即2x-5<-x+1.
点评 本题考查了一次函数与一元一次不等式的关系,从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了一次函数与一元一次方程的关系.

练习册系列答案
相关题目
5.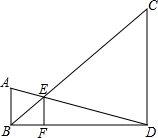 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
17. 如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
 如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
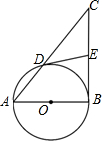 如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.
如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE. (1)画出图中的10块小立方块搭成几何体的主视图、左视图和俯视图.
(1)画出图中的10块小立方块搭成几何体的主视图、左视图和俯视图.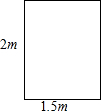 如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽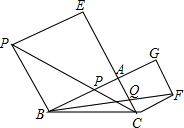 如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.
如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.