题目内容
6.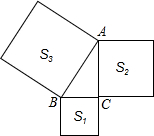 如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=6,S3=18,则S2=12.
如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=6,S3=18,则S2=12.
分析 由三角形ABC为直角三角形,利用勾股定理列出关系式,结合正方形面积公式得到S3=S1+S2,即可求出S2的值.
解答 解:∵△ABC为直角三角形,
∴AB2=AC2+BC2,
∵以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=6,S3=18,
∴S3=S1+S2,
则S2=S3-S1=18-6=12,
故答案为:12
点评 此题考查了勾股定理,以及正方形的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
17. 如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
 如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
1.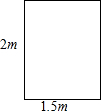 如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.8m.可以从这扇门通过的木板是
( )
 如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.8m.可以从这扇门通过的木板是
( )
| A. | ①号 | B. | ②号 | C. | ③号 | D. | 均不能通过 |
16.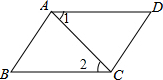 如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
 如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )| A. | AB=DC | B. | ∠1=∠2 | C. | AB=AD | D. | ∠D=∠B |
 (1)画出图中的10块小立方块搭成几何体的主视图、左视图和俯视图.
(1)画出图中的10块小立方块搭成几何体的主视图、左视图和俯视图.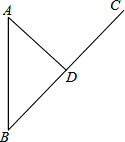 如图,某沿海城市A接到台风警报,在该市正南方向$120\sqrt{2}$km有一台风中心正在B处形成,并沿着北偏东45°的BC方向以15km/h的速度向C移动,AD⊥BC于D,如果在距台风中心150km的区域内都将受到台风的影响,请问:
如图,某沿海城市A接到台风警报,在该市正南方向$120\sqrt{2}$km有一台风中心正在B处形成,并沿着北偏东45°的BC方向以15km/h的速度向C移动,AD⊥BC于D,如果在距台风中心150km的区域内都将受到台风的影响,请问: