题目内容
7.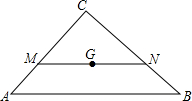 已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )
已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )| A. | 3 | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
分析 由MN∥AB易得△CMN∽△CAB,同理可证△CMG∽△CAD,所以$\frac{MN}{AB}=\frac{CM}{CA}=\frac{CG}{CD}$,由G是三角形的重心知$\frac{CG}{CD}=\frac{2}{3}$,即可求MN的长.
解答 解:如图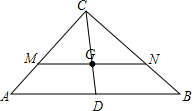 所示,连接CD,
所示,连接CD,
∵MN∥AB,
∴∠CMN=∠A,∠CNM=∠B,
∴△CMN∽△CAB,
同理可证△CMG∽△CAD,
∴$\frac{MN}{AB}=\frac{CM}{CA}=\frac{CG}{CD}$,
又∵G是三角形的重心,
∴$\frac{CG}{CD}=\frac{2}{3}$,
∴$\frac{MN}{AB}$=$\frac{MC}{AC}$=$\frac{CG}{CD}$=$\frac{2}{3}$,
∴MN=$\frac{2}{3}$AB=$\frac{2}{3}$×$\frac{15}{2}$=5.
故选:D.
点评 本题主要考查了三角形的重心的性质,相似三角形的判定及性质.①三角形三边的中线相交于一点,这点叫做三角形的重心.②重心到顶点的距离等于它到对边中点距离的两倍.③平行于三角形一边的直线截其它两边,所得三角形与原三角形相似.④相似三角形的三边对应成比例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
 如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,BC=8.则∠A的正切值等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
16.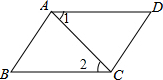 如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
 如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )| A. | AB=DC | B. | ∠1=∠2 | C. | AB=AD | D. | ∠D=∠B |
17.下列运算,结果正确的是( )
| A. | m2+m2=m4 | B. | (m+$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$ | C. | (3mn2)2=6m2n4 | D. | 2m2n÷$\frac{m}{n}$=2mn2 |
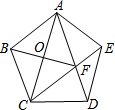 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.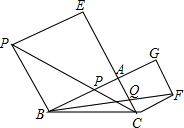 如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.
如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.