题目内容
6.计算(1)|$\root{3}{27}$|+|-$\sqrt{16}$|+$\sqrt{4}$-$\root{3}{8}$
(2)化简:|1-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|+|$\sqrt{3}$-2|
分析 (1)原式利用平方根、立方根定义,以及绝对值的代数意义化简即可得到结果;
(2)原式利用绝对值的代数意义化简即可得到结果.
解答 解:(1)原式=3+4+2-2=7;
(2)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$=1.
点评 此题考查了实数的运算,绝对值,以及平方根、立方根,熟练掌握各自的性质是解本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
18.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的有( )
①$\frac{c}{a}$=6;②函数y=ax2+bx+c的最小值为-6;③抛物线的对称轴是x=$\frac{7}{2}$;④方程ax2+bx+c=0有两个正整数解.
| x | … | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 0 | -3 | -6 | -6 | -3 | … |
①$\frac{c}{a}$=6;②函数y=ax2+bx+c的最小值为-6;③抛物线的对称轴是x=$\frac{7}{2}$;④方程ax2+bx+c=0有两个正整数解.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.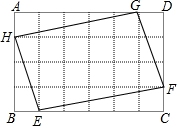 如图,矩形ABCD是由24个大小相等的正方形组成的,?EFGH的四个顶点分别在BC,CD,AD,AB边上,且是某个小正方形的顶点,若?EFGH的面积为32,则矩形ABCD的面积为( )
如图,矩形ABCD是由24个大小相等的正方形组成的,?EFGH的四个顶点分别在BC,CD,AD,AB边上,且是某个小正方形的顶点,若?EFGH的面积为32,则矩形ABCD的面积为( )
 如图,矩形ABCD是由24个大小相等的正方形组成的,?EFGH的四个顶点分别在BC,CD,AD,AB边上,且是某个小正方形的顶点,若?EFGH的面积为32,则矩形ABCD的面积为( )
如图,矩形ABCD是由24个大小相等的正方形组成的,?EFGH的四个顶点分别在BC,CD,AD,AB边上,且是某个小正方形的顶点,若?EFGH的面积为32,则矩形ABCD的面积为( )| A. | 24$\sqrt{2}$ | B. | 12$\sqrt{22}$ | C. | 24 | D. | 48 |
 如图,将长方形ABCD分割成1个灰色长方形与52个边长为1的小正方形,若灰色长方形的长与宽之比为7:5,则灰色长方形的长为14.
如图,将长方形ABCD分割成1个灰色长方形与52个边长为1的小正方形,若灰色长方形的长与宽之比为7:5,则灰色长方形的长为14.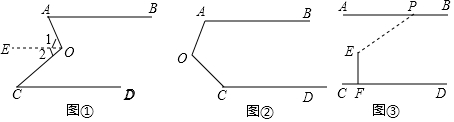
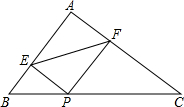 如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为4.8.
如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为4.8.