题目内容
15.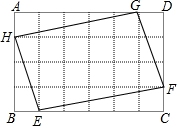 如图,矩形ABCD是由24个大小相等的正方形组成的,?EFGH的四个顶点分别在BC,CD,AD,AB边上,且是某个小正方形的顶点,若?EFGH的面积为32,则矩形ABCD的面积为( )
如图,矩形ABCD是由24个大小相等的正方形组成的,?EFGH的四个顶点分别在BC,CD,AD,AB边上,且是某个小正方形的顶点,若?EFGH的面积为32,则矩形ABCD的面积为( )| A. | 24$\sqrt{2}$ | B. | 12$\sqrt{22}$ | C. | 24 | D. | 48 |
分析 设小正方形的边长为a,根据四边形EFGH的面积可由矩形ABCD的面积减去四角的小直角三角形的面积,列出方程即可解决问题.
解答 解:设小正方形的边长为a,易知△AEF≌△CGH,△DEH≌△BGF;
故S阴影=S矩形-2(S△AEF+S△DEH)
32=24a2-2×($\frac{1}{2}$×a×3a+$\frac{1}{2}$×a×5a),
解得a2=2,
∴矩形ABCD的面积为48
故选D.
点评 此题矩形的性质、全等三角形的判定和性质、三角形的面积公式等知识,解答此题的关键是学会构建方程解决问题,属于中考常考题型.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
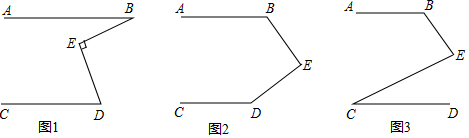
10. 如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )
如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )
 如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )
如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |