题目内容
3.有5张卡,分别写有数字2,3,4,5,6,如果允许6可以作9用,那么从中任意取出3张卡片,并排放在一起,问:可以组成多少个不同的三位偶数?分析 先考虑6只能当6的所有情况数,再考虑6作为9用的所有可能情况,根据乘法原理即可求出组成不同的三位偶数的所有可能结果.
解答 解:先考虑6只能当6的情况,分三步取出卡片.
首先因为组成的三位数是偶数,个位数字只能是偶数,所以先选取最右边的也就是个位数位置上的卡片,有2、4、6三种不同的选择;
第二步在其余的4张卡片中任取一张,放在十位数的位置上,有4种不同的选法;
最后从剩下的3张卡片中选取一张,放在百位数的位置上,有3种不同的选择.根据乘法原理,6只是6时,可以组成3×4×3=36(个)不同的三位偶数;
这时候算所求的三位偶数并不是简单乘以2就可以的,
因为如果个位是6的话变成9就不再是偶数,多乘的还需要减去,个位是6一共有4×3=12(个)不同的三位偶数,
所以,可以组成36×2-12=60(个)不同的三位偶数.
点评 本题考查了求随机事件的概率,用到的知识点有乘法原理:完成一件事,这个事情可以分成n个必不可少的步骤:第1步有A种不同的方法,第二步有B种不同的方法…第n步有N种不同的方法.那么完成这件事情一共有A×B×…×N种不同的方法.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
12.甲班有学生48人,乙班有学生42人,要使两班的人数相等,设从甲班凋x人到乙班,则得方程( )
| A. | 48-x=42-x | B. | 48-x=42+x | C. | 48-x=2(42+x) | D. | 以上都不对 |
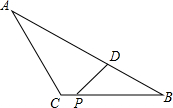 如图,在△ABC中,AB=6,BC=4,AC=3,点P在边BC上运动(不含点B),过点P作∠DPB=∠A,PD交AB于点D吗,设PB=x,AD=y
如图,在△ABC中,AB=6,BC=4,AC=3,点P在边BC上运动(不含点B),过点P作∠DPB=∠A,PD交AB于点D吗,设PB=x,AD=y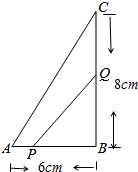 如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动.
如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动. 如图,某公路上有A、B、C三站,一辆汽车在上午8时从高A站5km的P地出发向C站匀速行驶,15min后离A站20km
如图,某公路上有A、B、C三站,一辆汽车在上午8时从高A站5km的P地出发向C站匀速行驶,15min后离A站20km