题目内容
11.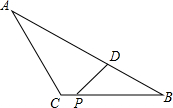 如图,在△ABC中,AB=6,BC=4,AC=3,点P在边BC上运动(不含点B),过点P作∠DPB=∠A,PD交AB于点D吗,设PB=x,AD=y
如图,在△ABC中,AB=6,BC=4,AC=3,点P在边BC上运动(不含点B),过点P作∠DPB=∠A,PD交AB于点D吗,设PB=x,AD=y(1)求y关于x的函数表达式和自变量x的取值范围
(2)当x取何值时,y最小?最小值是多少?
分析 (1)由∠DPB=∠A,∠B=∠B,得到△ABC∽△PBD,根据相似三角形的性质得到$\frac{AB}{PB}=\frac{BC}{BD}$,代入数据即可得到结论;
(2)根据一次函数的性质得到y随x的增大而减小,由于0<x≤4,于是得到当x=4时,y最小,即可得到结论.
解答 解:(1)∵∠DPB=∠A,∠B=∠B,
∴△ABC∽△PBD,
∴$\frac{AB}{PB}=\frac{BC}{BD}$,
∵AB=6,BC=4,AC=3,PB=x,AD=y,
∴BD=6-y,
∴$\frac{6}{x}=\frac{4}{6-y}$,
∴y=-$\frac{2}{3}$x+6;
(2)∵y=-$\frac{2}{3}$x+6,
∵k=-$\frac{2}{3}$<0,
∴y随x的增大而减小,
∵0<x≤4,
∴当x=4时,y最小,
∴y最小=$\frac{10}{3}$.
点评 本题考查了相似三角形的判定和性质,求函数的解析式,最值问题,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
2.下列四组线段中,可构成直角三角形的是( )
| A. | 1.5,2,2.5 | B. | 1,2,3 | C. | 1,$\sqrt{2}$,3 | D. | 2,3,4 |
19.规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,就称此图形为旋转对称图形,那么下列图形中是旋转对称图形,且有一个旋转角为60°的是( )
| A. | 正八边形 | B. | 正六边形 | C. | 正方形 | D. | 正三角形 |




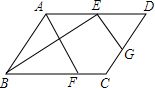 如图,在?ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,求AF的长.
如图,在?ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,求AF的长.