题目内容
15. 如图,某公路上有A、B、C三站,一辆汽车在上午8时从高A站5km的P地出发向C站匀速行驶,15min后离A站20km
如图,某公路上有A、B、C三站,一辆汽车在上午8时从高A站5km的P地出发向C站匀速行驶,15min后离A站20km(1)设出发xh后,汽车离A站ykm,写出y与x之间的函数表达式;
(2)当汽车行驶到离A站215km的B站时,接到通知要在中午12点前赶到离B站35km的C站,汽车若按原速能否按时到达?若能,是在几时几分到达?若不能,车速最少应提高到多少?
分析 (1)首先根据15分钟后离A站20千米,求得汽车每小时的速度,再根据路程=速度×时间,进行分析;
(2)根据(1)中的函数关系式求得x的值,即可分析汽车若按原速能否按时到达;若不能,设汽车按时到达C站,车速最少应提高到每小时V千米.根据路程=速度×时间,列方程求解.
解答 解:(1)汽车匀速前进的速度为:(20-5)÷$\frac{15}{60}$=60(千米/时),
∴y=60x+5.
(2)当y=215+35=250时,
60x+5=250,
解得x=$\frac{49}{12}$(小时)
8+4$\frac{1}{12}$=12$\frac{1}{12}$,
因此汽车若按原速不能按时到达.
当y=215时,
60x+5=215,
解得x=3.5(小时)
设汽车按时到达C站,车速最少应提高到每小时V千米.
依题,得[(12-8)-3.5]V=35,
∴V=70(千米/时).
故车速最少应提高到每小时70千米.
点评 此题考查一次函数的实际运用,掌握行程问题中的基本数量关系,建立函数是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
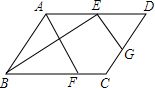 如图,在?ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,求AF的长.
如图,在?ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,求AF的长.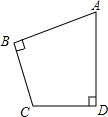 如图,在四边形ABCD中,∠ABC=∠ADC=90°,
如图,在四边形ABCD中,∠ABC=∠ADC=90°,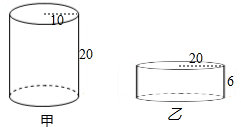 如图所示,有甲、乙两个容器,甲容器盛满了水,乙容器里没有水,现将甲容器中的水全部倒入乙容器,问:乙容器的水会不会溢出?如果不会溢出,请你求出倒入水后乙容器的水深;如果水会溢出,请你说明理由.(图中数据的单位:cm)
如图所示,有甲、乙两个容器,甲容器盛满了水,乙容器里没有水,现将甲容器中的水全部倒入乙容器,问:乙容器的水会不会溢出?如果不会溢出,请你求出倒入水后乙容器的水深;如果水会溢出,请你说明理由.(图中数据的单位:cm)