题目内容
2. 如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
分析 认真审题,根据垂线段最短得出PM⊥AB时线段PM最短,分别求出PB、OB、OA、AB的长度,利用△PBM∽△ABO,即可求出本题的答案.
解答 解:如图,过点P作PM⊥AB,则:∠PMB=90°,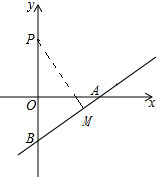
当PM⊥AB时,PM最短,
因为直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,
可得点A的坐标为(4,0),点B的坐标为(0,-3),
在Rt△AOB中,AO=4,BO=3,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵∠BMP=∠AOB=90°,∠B=∠B,PB=OP+OB=7,
∴△PBM∽△ABO,
∴$\frac{PB}{AB}$=$\frac{PM}{AO}$,
即:$\frac{7}{5}=\frac{PM}{4}$,
所以可得:PM=$\frac{28}{5}$.
点评 本题主要考查了垂线段最短,以及三角形相似的性质与判定等知识点,是综合性比较强的题目,注意认真总结.

练习册系列答案
相关题目
10.今年我市计划扩大城区绿地面积,现有一块长方形绿地,它的短边长为60m,若将短边增大到与长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加1600m2.设扩大后的正方形绿地边长为x m,下面所列方程正确的是( )
| A. | x(x-60)=1600 | B. | x(x+60)=1600 | C. | 60(x+60)=1600 | D. | 60(x-60)=1600 |
14.为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):-6,-3,x,2,-1,3.若这组数据的中位数是-1,则下列结论错误的是( )
| A. | 方差是8 | B. | 极差是9 | C. | 众数是-1 | D. | 平均数是-1 |
 在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图. 如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.
如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D. 在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)
在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)