题目内容
6.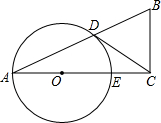 如图,在△ABC中,∠ACB=90°,点O为边AC上一点,以O为圆心AO为半径的⊙O与AB相交于点D,且CD与圆O相切于点D.
如图,在△ABC中,∠ACB=90°,点O为边AC上一点,以O为圆心AO为半径的⊙O与AB相交于点D,且CD与圆O相切于点D.(1)求证:CD=CB;
(2)若CE=2,CB=3,求sinA.
分析 (1)连接OD,由切线的性质得到∠CDO=90°,于是得到∠ADO+∠BDC=90°,根据直角三角形的性质得到∠A+∠B=90°,由等腰三角形的性质得到∠A=∠ADO,等量代换得到∠BDC=∠B,即可得到结论;
(2)设⊙O的半径为r,根据勾股定理得到r=$\frac{5}{4}$,求得AE=$\frac{5}{2}$,AC=$\frac{9}{2}$,由勾股定理得到AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=3$\sqrt{5}$,根据三角函数的定义即可得到结论.
解答 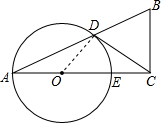 解:(1)连接OD,
解:(1)连接OD,
∵CD与圆O相切于点D,
∴∠CDO=90°,
∴∠ADO+∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∵OD=OA,
∴∠A=∠ADO,
∴∠BDC=∠B,
∴CD=CB;
(2)设⊙O的半径为r,
∴OD=OE=r,
∵CE=2,CB=3,
∴CD=3,OC=2+r,
∴r2+32=(2+r)2,
∴r=$\frac{5}{4}$,
∴AE=$\frac{5}{2}$,∴AC=$\frac{9}{2}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=3$\sqrt{5}$,
∴sinA=$\frac{BC}{AB}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查了切线的性质、等腰三角形的性质、勾股定理;熟练掌握切线的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
11.某市2014年的国民生产总值为2037亿元,这个数用科学记数法表示为( )
| A. | 2.037×1010元 | B. | 2.037×1011元 | C. | 2.037×1012元 | D. | 20.37×1010元 |
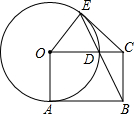 如图所示,在矩形OABC中,以O为圆心,OA为半径作圆,交OC,于点D,连接BD并延长,交⊙O于点E,连接OE,EC,EC=BC.
如图所示,在矩形OABC中,以O为圆心,OA为半径作圆,交OC,于点D,连接BD并延长,交⊙O于点E,连接OE,EC,EC=BC.