题目内容
18.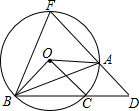 如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF∥OC,交BC的延长线于点D,交⊙O于点F,连接BF.
如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF∥OC,交BC的延长线于点D,交⊙O于点F,连接BF.(1)求证:∠BAC=2∠ABC;
(2)若∠BAC=40°,AB=3.2,BD=4.
①求∠BAF的度数;②求$\frac{AF}{BF}$的值.
分析 (1)根据圆周角定理和等量代换即可得到结论.
(2)①根据∠BAC=$\frac{1}{2}$∠BOC,∠BAC=40°,求得∠BOC=2∠BAC=80°,由(1)知,∠BAC=2∠ABC,于是得到∠ABC=20°,∠ACD=∠BAC+∠ABC=60°,由四边形AFBC是⊙O的内接四边形,得到∠F=∠ACD=60°,由于OB=OC,求得∠OBC=∠OCB=$\frac{1}{2}$(180°-80°)=50°,根据平行线的性质得到∠D=∠OCB=50°,由于∠DBF=180°-∠F-∠D,于是求得∠DBF=180°-60°-50°=70°;
②由①得∠ABC=20°,∠D=50°,证得∠BAF=∠DBF,由于∠F=∠F,推出△ABF∽△BDF,即可得到结论.
解答 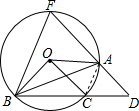 (1)证明:连接AC,
(1)证明:连接AC,
∵∠BAC=$\frac{1}{2}$∠BOC,∠ABC=$\frac{1}{2}$∠AOC,∠BOC=2∠AOC,
∴∠BAC=∠AOC=2∠ABC;
(2)解:①∵∠BAC=$\frac{1}{2}$∠BOC,∠BAC=40°,
∴∠BOC=2∠BAC=80°,由(1)知,∠BAC=2∠ABC,
∴∠ABC=20°,
∴∠ACD=∠BAC+∠ABC=60°,
∵四边形AFBC是⊙O的内接四边形,
∴∠F=∠ACD=60°,
∵OB=OC,
∴∠OBC=∠OCB=$\frac{1}{2}$(180°-80°)=50°,
∵DF∥OC,
∴∠D=∠OCB=50°,
∵∠DBF=180°-∠F-∠D,
∴∠DBF=180°-60°-50°=70°,
②由①得∠ABC=20°,∠D=50°,
∴∠BAF=∠ABD+∠D=20°+50°=70°,
∵∠DBF=70°,
∴∠BAF=∠DBF,
∵∠F=∠F,
∴△ABF∽△BDF,
∴$\frac{AB}{BD}=\frac{AF}{BF}$=$\frac{3.2}{4}$=$\frac{4}{5}$.
点评 本题考查了相似三角形的判定和性质,圆周角定理,圆内接四边形的性质,平行线的性质,熟练掌握这些定理是解题的关键.

 阅读快车系列答案
阅读快车系列答案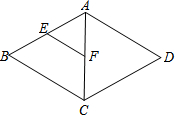 如图所示,在菱形ABCD中,点E,F分别是AB,AC的中点,如果菱形的周长为16,那么EF等于( )
如图所示,在菱形ABCD中,点E,F分别是AB,AC的中点,如果菱形的周长为16,那么EF等于( )| A. | 4 | B. | 8 | C. | 12 | D. | 2 |
| A. | (a+b+10)(a+b-2) | B. | (a+b+5)(a+b-4) | C. | (a+b+2)(a+b-10) | D. | (a+b+4)(a+b-5) |

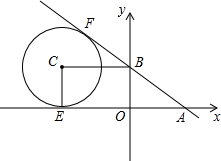 如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.
如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.