题目内容
9.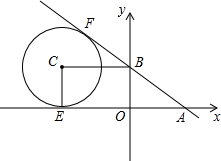 如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.
如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.(1)则A、B两点的坐标分别为:A(4,0),B(0,3).(直接写答案,不需要写过程)
(2)如果⊙P与x轴、y轴、直线AB都相切,则这样的⊙P共有3个,其中最小的圆的半径为1.(直接写答案,不需要写过程)
(3)如果点C(m,n)在第二象限,以点C(m,n)为圆心的⊙C与直线AB相切,与x轴相切于点E,
①若四边形CEOB为矩形,求C点的坐标;
②求m与n之间的函数关系式.
分析 (1)因为直线y=-$\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B,所以分别令x=0,y=0,可求出A(4,0),B(0,3);
(2)在一、二、四三个象限中都有与坐标轴相切的三个圆,在第一象限内最小,利用圆的内切圆的半径的求法求得半径即可;
(3)①根据点A和点B的坐标得到OA=4,OB=3,AB=5,连接CF,当四边形OBCE为矩形时,有CF=CE=OB=3,CB∥x轴,利用两直线平行同位角相等可得∠CBF=∠BAO,又因为⊙C与直线AB相切于点F,所以CF⊥AB于点F,利用AAS可知△CBF≌△BAO,所以CB=AB=5,即点C的坐标为(-5,3);
②因为点C(m,n)是第二象限内任意一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F,所以可延长EC交AB于G,连接CF,则CF=CE=n,因为⊙C与x轴相切于点E,所以GE⊥AE于点E,EG∥y轴,∠CGF=∠OBA,所以可证△FCG∽△OAB,$\frac{CF}{OA}$=$\frac{CG}{AB}$,即CG=$\frac{5}{4}$n,又因GE=CG+CE=$\frac{5}{4}$=$\frac{9}{4}$n,AE=OA+OE=4-m,利用tan∠EAG=tan∠BAO,即可得到关于m、n的关系式$\frac{\frac{9}{4}n}{4-m}$=$\frac{3}{4}$,整理即可;
解答 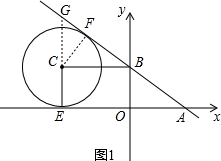 解:(1)如图1,
解:(1)如图1,
当x=0时,y=3;
当y=0时,x=4;
∴A(4,0),B(0,3);
(2)如果⊙P与x轴、y轴、直线AB都相切,
则这样的⊙P共有3个,其中最小的圆是在第一象限时,
此时⊙P是△AOB的内切圆,半径为$\frac{3+4-5}{2}$=1;
(3)①∵A(4,0),B(0,3),
∴OA=4,OB=3,AB=5,
连接CF,
当四边形OBCE为矩形时,有CF=CE=OB=3,CB∥x轴,
∴∠CBF=∠BAO
∵⊙C与直线AB相切于点F,
∴CF⊥AB于点F
∴∠CFB=∠BOA,
又∵CF=OB,
∴△CBF≌△BAO,
∴CB=AB=5,
∴点C的坐标为(-5,3);
②如图1,延长EC交AB于G,连接CF,则CF=CE=n,
∵⊙C与x轴相切于点E,
∴GE⊥AE于点E,
∴EG∥y轴,
∴∠CGF=∠OBA,
又由(1)得∠GFC=∠BOA=90°,
∴△FCG∽△OAB,
∴$\frac{CF}{OA}$=$\frac{CG}{AB}$,
∴CG=$\frac{5}{4}$n,
又∵GE=CG+CE=$\frac{5}{4}$n+n=$\frac{9}{4}$n,
又∵AE=OA+OE=4-m,
∴在Rt△AEG中,tan∠EAG=$\frac{GE}{AE}$=$\frac{\frac{9}{4}n}{4-m}$,
在Rt△AOB中,tan∠BAO=$\frac{OB}{ON}$=$\frac{3}{4}$,
∴$\frac{\frac{9}{4}n}{4-m}$=$\frac{3}{4}$,
∴m=4-3n;
点评 本题考查了矩形的性质和判定,一次函数的应用,勾股定理,相似三角形的性质和判定,矩形的性质,切线长定理,切线的性质,坐标与图形性质等知识点的运用,能综合运用性质进行推理和计算是解此题的关键,题目综合性比较强,有一定的难度.

| A. | (-3,-1) | B. | (11,6) | C. | (3,2) | D. | (4,3) |
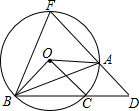 如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF∥OC,交BC的延长线于点D,交⊙O于点F,连接BF.
如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF∥OC,交BC的延长线于点D,交⊙O于点F,连接BF.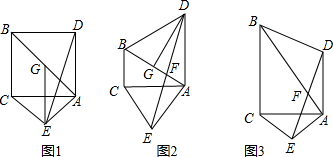
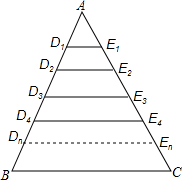 如图,△ABC中,BC=a.
如图,△ABC中,BC=a.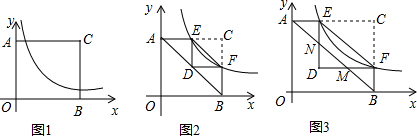
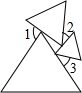 三个等边三角形的位置如图所示,若∠3=40°,则∠1+∠2=140°.
三个等边三角形的位置如图所示,若∠3=40°,则∠1+∠2=140°.