题目内容
10.如果x>$\sqrt{2}$x+1,化简:$\sqrt{(x+\sqrt{2})^{2}}$-$\sqrt{(x+\sqrt{2}+1)^{2}}$.分析 先根据x>$\sqrt{2}$x+1,确定x的取值范围,再进行化简,即可解答.
解答 解:x>$\sqrt{2}$x+1,
x-$\sqrt{2}$x>1
x(1-$\sqrt{2}$)>1,
x<$\frac{1}{1-\sqrt{2}}$
x<-($\sqrt{2}$+1),
∴x+$\sqrt{2}$<0,x+$\sqrt{2}$+1<0,
∴$\sqrt{(x+\sqrt{2})^{2}}$-$\sqrt{(x+\sqrt{2}+1)^{2}}$=-(x+$\sqrt{2}$)+(x$+\sqrt{2}$+1)=-x-$\sqrt{2}$+x+$\sqrt{2}$+1=1.
点评 本题考查了二次根式的性质与化简,解决本题的关键是熟记二次根式的性质.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
20.下列说法中,错误的是( )
| A. | 不等式x<2的正整数解有一个 | B. | -2是不等式2x-1<0的一个解 | ||
| C. | 不等式x<10的整数解有无数个 | D. | 不等式2x>-6的解集是x<-3 |
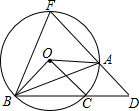 如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF∥OC,交BC的延长线于点D,交⊙O于点F,连接BF.
如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF∥OC,交BC的延长线于点D,交⊙O于点F,连接BF.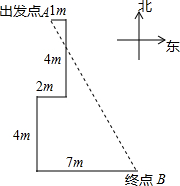 如图,小明从点A出发,先向东走1m,然后向南走4m,再向西走2m,最后向东走7m,达到点B,求出发点A到终点B的距离.
如图,小明从点A出发,先向东走1m,然后向南走4m,再向西走2m,最后向东走7m,达到点B,求出发点A到终点B的距离.