题目内容
5.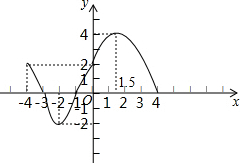 已知某一函数的全部图象如图所示,根据图象回答下列问题:
已知某一函数的全部图象如图所示,根据图象回答下列问题:(1)确定自变量x的取值范围,-4≤x≤4;
(2)当x=-4时,y的值是2;
(3)当y=0时,x的值是-3,-1,4;
(4)当x=1.5时,y的值最大,当x=-2时,y的值最小;
(5)当x的值在什么范围内时y随x的增大而增大?答:-2≤x≤1.5;
(6)当x的值在什么范围内时,y<0,答-3<x<-1.
分析 (1)根据函数图象的横坐标,可得答案;
(2)根据自变量的值与函数值的对应关系,可得相应的函数值;
(3)根据函数值,可得相应自变量的值;
(4)根据函数图象的最高点、最低点,可得相应自变量的值;
(5)根据函数图象的横坐标,可得函数的增区间;
(6)根据函数图象在x轴下方的部分函数值小于零,可得答案.
解答 解:(1)确定自变量x的取值范围,-4≤x≤4;
(2)当x=-4时,y的值是 2;
(3)当y=0时,x的值是-3,-1,4;
(4)当x=1.5时,y的值最大,当x=-2时,y的值最小;
(5)当x的值在什么范围内时y随x的增大而增大?答:-2≤x≤1.5;
(6)当x的值在什么范围内时,y<0,答-3<x<-1;
故答案为:-4≤x≤4;2;-3,4;1.5,-2;-2≤x≤1.5;-3<x<-1.
点评 本题考查了函数图象,观察函数图象的变化趋势获得有效信息是解题关键.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
16.2013年入春以来,北方部分地区干旱严重,导致凤凰社区人畜饮用水紧张.每天需从社区外调运饮用水120吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点.甲厂每天最多可调出80吨.乙厂每天最多可调出90吨.从两水厂运水到凤凰社区供水点的路程和运费如下表:
(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运饮用水多少吨?
(2)设从甲厂调运饮用水x吨.总运费为w元.试写出w与x的函数关系式.
(3)怎样安排调运方案才能使每天的总运费最省?
| 到凤凰社区供水点的路程(千米) | 运费(元/吨•千米) | |
| 甲厂 | 20 | 12 |
| 乙厂 | 14 | 15 |
(2)设从甲厂调运饮用水x吨.总运费为w元.试写出w与x的函数关系式.
(3)怎样安排调运方案才能使每天的总运费最省?
13.将抛物线$y=-\frac{1}{2}{x^2}$+2x+1的顶点坐标为( )
| A. | (2,3) | B. | (-2,-3) | C. | (-2,-1) | D. | (2,-3) |
17.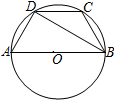 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )| A. | 25πcm2 | B. | 49πcm2 | C. | 32πcm2 | D. | 36πcm2 |
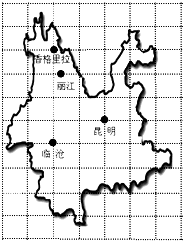 北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).
北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).
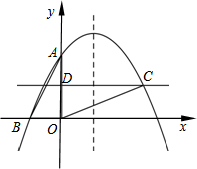 如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.
如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.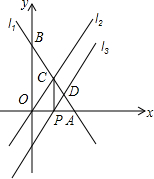 如图,已知直线l1:y=-2x+8与两坐标轴分别相交于A、B两点,与直线l2:y=2x相交于点C,点P为x轴上的一个动点,过点P的直线,l3∥l2,且与l1相交于点D.
如图,已知直线l1:y=-2x+8与两坐标轴分别相交于A、B两点,与直线l2:y=2x相交于点C,点P为x轴上的一个动点,过点P的直线,l3∥l2,且与l1相交于点D.