题目内容
13.将抛物线$y=-\frac{1}{2}{x^2}$+2x+1的顶点坐标为( )| A. | (2,3) | B. | (-2,-3) | C. | (-2,-1) | D. | (2,-3) |
分析 已知抛物线的解析式是一般式,用配方法转化为顶点式,根据顶点式的坐标特点,直接写出顶点坐标.
解答 解:∵$y=-\frac{1}{2}{x^2}$+2x+1=-$\frac{1}{2}$(x2-4x)+1=-$\frac{1}{2}$(x-2)2+3,
∴顶点坐标是(2,3).
故选A.
点评 此题主要考查了二次函数的性质,二次函数y=a(x-h)2+k的顶点坐标为(h,k),对称轴为x=h,此题还考查了配方法求顶点式.

练习册系列答案
相关题目
4.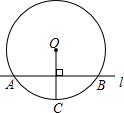 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
18. 如图所示,若a∥b,∠1=120°,则∠2=( )
如图所示,若a∥b,∠1=120°,则∠2=( )
 如图所示,若a∥b,∠1=120°,则∠2=( )
如图所示,若a∥b,∠1=120°,则∠2=( )| A. | 55° | B. | 60° | C. | 65° | D. | 75° |
2.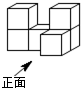 如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
 如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
如图是由6个完全相同的小正方体组成的几何体,其左视图为( )| A. | 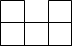 | B. | 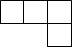 | C. | 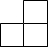 | D. | 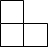 |
 如图,长方体的长、宽、高分别为8、4、5,一只蚂蚁沿长方体表面从顶点A爬到顶点B,则它走过的路程最短为$\sqrt{145}$.
如图,长方体的长、宽、高分别为8、4、5,一只蚂蚁沿长方体表面从顶点A爬到顶点B,则它走过的路程最短为$\sqrt{145}$.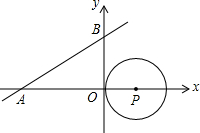 直线y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左平移,当圆P与该直线相切时点P的坐标为(-1,0)或(-5,0);当圆P与该直线相交时,横坐标为整数的点P有3个.
直线y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左平移,当圆P与该直线相切时点P的坐标为(-1,0)或(-5,0);当圆P与该直线相交时,横坐标为整数的点P有3个. 已知某一函数的全部图象如图所示,根据图象回答下列问题:
已知某一函数的全部图象如图所示,根据图象回答下列问题: